Perdite di carico nelle condotte
E' noto come,
l'equazione di Bernoulli sia valida soltanto nel caso di liquidi
ideali.
Nel caso di liquidi reali, anche a causa della viscosità,
si instaurano degli attriti; queste dissipazioni di energia vengono
denominate perdite di carico. Possono
esserci perdite di carico continue (distribuite) o perdite di carico
accidentali (localizzate ).
Le perdite di carico continue, anche semplicemente attribuibili alla viscosità, sono compendiate dalla nota formula di Darcy-Weisbach:
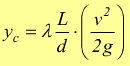 [mca]
(m di colonna d'acqua) considerando
[mca]
(m di colonna d'acqua) considerando
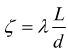
L : lunghezza del tubo
d : diametro del tubo
v : velocità del fluido
g : accelerazione di gravità
ζ è chiamato coefficiente di attrito, esso contiene il fattore di attrito λ (Darcy friction factor) .
Se il moto è in regime laminare:
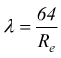 con Re numero
di Reynolds
con Re numero
di Reynolds
Così l'equazione di Bernoulli può essere modificata come
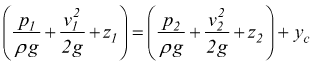

Se siamo in regime turbolento, il valore del fattore attrito λ risulta funzione del numero di Reynolds e della rugosità relativa del tubo, che risulta essere
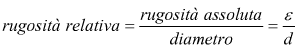
In questo caso bisogna usare l'equazione di Colebrook-White, che però, è una funzione implicita, difficile da calcolare manualmente;
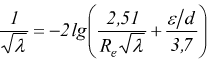
in alternativa si può usare la formula approssimata di Haaland :
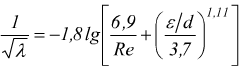
oppure si può usare il diagramma
di Moody.
Nel seguente caso viene eseguita la procedura di calcolo automatico tramite
approssimazioni successive, per l'individuazione di λ e del numero
di Reynolds.
q [l/s] portata
d [mm] diametro
ε [mm] rugosità assoluta
υ [m2/sec] viscosità cinematica
In fondo alla pagina è riportato un esempio di calcolo iterativo di lambda; per l'equazione di Colebrook.
Nella formula di Colebrook, si può osservare che :
1) per tubi nuovi e lisci ε/d molto piccolo 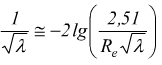
2) per un valore del numero di Reynolds Re molto grande
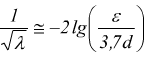
Inoltre dalla formula di Darcy 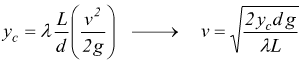
sostituendo nella formula del numero di Reynolds
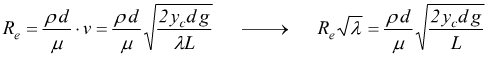
Quindi se sono note le perdite di carico si può risalire al prodotto ![]() dal
quale si può ottenere λ anche usando diagrammi di questo
tipo, attribuibile ad Hunter-Rosen.
dal
quale si può ottenere λ anche usando diagrammi di questo
tipo, attribuibile ad Hunter-Rosen.
Valori indicativi della rugosità assoluta (scabrezza) sono i seguenti:
| Materiale | ε [ μm ] (micrometri) |
| Tubi trafilati, piombo, vetro, ottone | 1,5 |
| PVC | 20 |
| Acciaio, ferro | 46 |
| Tubi in acciaio saldato | 46 |
| Ferro zincato | 150 |
| Ghisa | 250 |
| Cemento | 300÷3000 |
Per la soluzione a tentativi, conviene, normalmente, ipotizzare un numero di Reynolds molto alto, ad es. Re=200000 e poi approssimare λ progressivamente. Il calcolatore inserito qui sotto restituisce i valori del primo e del secondo membro dell'equazione di Colebrook segnalando quando la differenza tra i due è inferiore al 2%.
Associate alla perdite di carico nelle tubazioni, vi sono delle corrispondenti cadute di pressione, infatti se ci ricordiamo della legge di Stevin : p=ρgh.

normalmente interessa la caduta di pressione sull'unità di lunghezza:
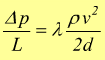 [
Pa/m ]
[
Pa/m ]
Un altro fatto di interesse è la potenza richiesta per mantenere in moto il liquido cioè per vincere la perdita di carico che è data dal prodotto fra la portata q e la caduta di pressione Δp.
![]()
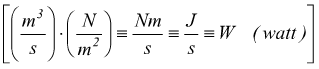
Le perdite di carico possono anche essere accidentali,dicevamo, in tal caso si usa solo la forma:
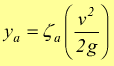 [mca]
[mca]
Dove ζa è il coefficiente di resistenza localizzata.
Le perdite di carico accidentali possono essere causate dalla presenza
di valvole da variazioni di direzione del flusso (curve) da improvvisi
restringimenti o allargamenti. Tutte le perdite di carico vanno sommate
quindi se indichiamo
ζc=perdite di carico continue
ζai=i-esima perdita di carico accidentale
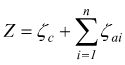 e
poi
e
poi 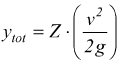
Valori rappresentativi del coefficiente di resistenza localizzata ζa sono:
| collegamento | |
|
| Valvola a globo, tutta aperta | 9 | |
| Valvola ad angolo, tutta aperta | 4 | |
| Valvola a saracinesca, tutta aperta | 0,26 | |
| Valvola a saracinesca, aperta a 3/4 | 0,7 | |
| Valvola a saracinesca, aperta a metà | 3,2 | |
| Valvola a saracinesca, aperta ad 1/4 | 18 | |
| Valvola di ritegno a cerniera, tutta aperta | 2,7 | |
| Valvola in linea a sfera, tutta aperta | 3 | |
| Valvola a farfalla, tutta aperta | 0,4 | |
| Gomito standard 90° | 0,6 | |
| Gomito standard 45° | 0,32 | |
| Gomito a raggio ampio 90° | 0,4 | |
| Gomito filettato 90° | 1 | |
| Gomito filettato 45° | 0,52 | |
| Giunto T, flusso nella direzione principale | 0,4 | |
| Giunto T, flusso attraverso la diramazione | 1,2 |
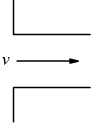
| Ingresso a spigolo vivo |
 |
|||||||||||||||
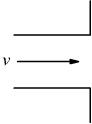
| Uscita a spigolo vivo |
 |
|||||||||||||||
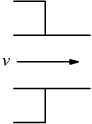
| Tubo rientrante |
 |
|||||||||||||||
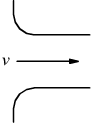
| Ingresso arrotondato |
 |
|||||||||||||||
| Riduzione brusca |
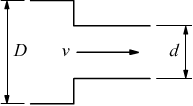 |
|
||||||||||||||
| Riduzione graduale |
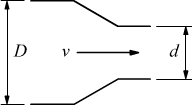 |
|||||||||||||||
| Allargamento brusco |
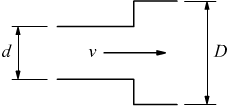 |
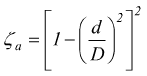 |
||||||||||||||
| Allargamento graduale | 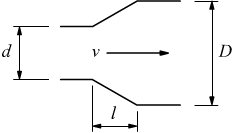 |
|
Formula pratica
La formula di Darcy ha una variante empirica:
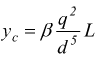
q=portata
d=diametro del tubo
L=lunghezza della tubazione
Il coefficiente β dipende dallo stato della condotta; di solito si pone:
β=0,00165 per tubi nuovi e lisci
β=0,002 per tubi in servizio corrente
β=0,0033 per tubi in servizio da molto tempo
se non si hanno informazioni sufficienti si pone:
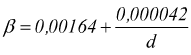
come suggerito dallo stesso Darcy.
d diametro
L [m] lunghezza
β
Formula di Colebrook
I dati del problema di esempio per il calcolo di λ con l'utilizzo della formula di Colebrook-White sono gli stessi, di default, proposti dal calcolatore:
portata q=55 l/s=0,055 m3/s
diametro d=400mm=0,4m
scabrezza ass. ε=3mm=0,003m
viscosità cinematica υ=0,00000114
il numero di Reynolds è 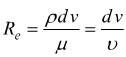
sapendo che la viscosità cinematica è 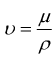 e
che la portata è
e
che la portata è
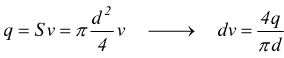 dunque
dunque
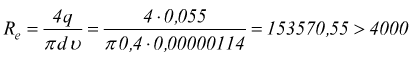 siamo
in regime turbolento
siamo
in regime turbolento
1° caso) essendo ε>0 calcolo il coefficiente λ1
di 1° tentativo ipotizzando il regime assolutamente turbolento.
In tale regime λ è indipendente da Re e dipende solamente
da ε/d, l'equazione di Colebrook-White si riduce a
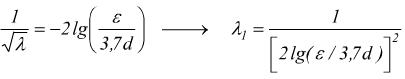
che va inserito nel 2° membro dell'equazione di Colebrook-White per ricavare il λ2 di secondo tentativo.
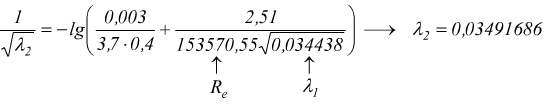
che va sostituito nel secondo membro per ottenere il λ3
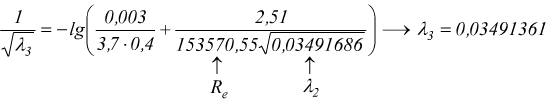
le iterazioni si arrestano quando la differenza percentuale λi+1-λi<1%
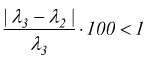
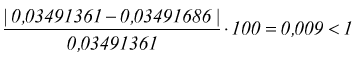
allora si assume λ=0,03491361≅0,035
2° caso) se la scabrezza ε=0 (tubi lisci).
Rimane, ovviamente, invariato il calcolo di Re. Invece il
valore del λ di 1° tentativo si può calcolare con la formula
di Filonenko-Altschuler
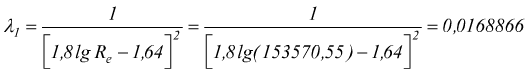
Il procedimento per il calcolo di λ2 λ3 .. è identico al caso precedente in cui ε>0.
 edutecnica
edutecnica