Idrodinamica
In un liquido in movimento, si riconoscono due tipi fondamentali di moto. Se il flusso è regolare, in modo tale che strati contigui (adiacenti) di liquido scivolino uno sull'altro si dice che si ha un moto laminare .
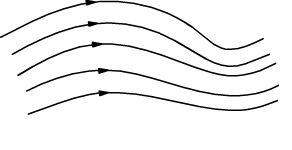
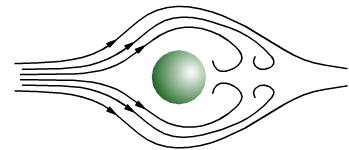
Nel moto laminare, ogni particella di liquido segue una traiettoria regolare chiamata linea di flusso che non incrocia mai le linee di flusso di altre particelle; la velocità della particella è sempre tangente alla linea di flusso.
Al di sopra di una certa velocità, il moto del liquido diventa turbolento.
Il moto turbolento, manifesta percorsi circolari
e vorticosi chiamati correnti a mulinello che assorbono molta energia
per l'attrito interno fra le particelle.
Si ha moto stazionario, quando
la velocità del liquido è costante in ogni punto dello spazio
(occupato dal liquido).
Numero di Reynolds
Il parametro che distingue il moto laminare dal moto turbolento è il
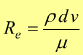 numero di Reynolds
numero di Reynolds

Il numero di Reynolds è adimensionale mentre della viscosità si sono
già viste alcune definizioni.
Per i liquidi in moto dentro le tubazioni, convenzionalmente è:
Re≤2000 :regime laminare
2000<Re<4000 : regime critico
Re≥4000 :regime turbolento
Portata
Se pensiamo ad un liquido in una conduttura, che si muove con moto laminare e stazionario, possiamo definirne la portata come il rapporto tra il volume ΔV di liquido che, nell'intervallo di tempo, attraversa una sezione trasversale della conduttura nell'intervallo Δt stesso.
 [
m3/sec ]
[
m3/sec ]
per contro, la corrente di un liquido si dice stazionaria quando la sua portata, attraverso qualunque sezione della conduttura è costante nel tempo.
Equazione di continuità
Per le condotte interessate da correnti stazionarie vale la relazione
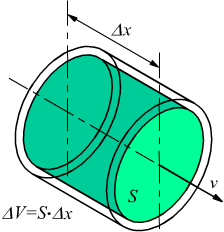
![]()
S=sezione della conduttura
v= velocità del fluido
E' facile verificare questa relazione; basta pensare ad un volume ΔV di liquido in moto a velocità costante v, lungo una condotta, bisogna ricordarsi che dimensionalmente la velocità è v=Δx/Δt.
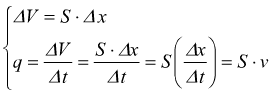
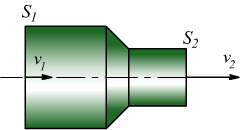
v1 [m/s]
d2 [m]
v2 [m/s]
Per due sezioni della conduttura S1 ed S2 dove il fluido si muove rispettivamente con velocità v1 e v2 vale l'equazione di continuità:
![]()
Abbiamo esperienza diretta di questa equazione, quando, annaffiando
il prato, usiamo mettere il dito davanti all'imboccatura della
canna dell'acqua per aumentare la velocità e la gittata del getto.
L'equazione di continuità può essere espressa anche tramite i
diametri


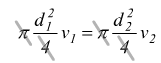
![]()
Equazione di Bernoulli
Se :
1) il fluido è incomprimibile
2) la corrente è stazionaria (regime permanente)
3) gli attriti sono trascurabili
si può applicare l'equazione di Bernoulli
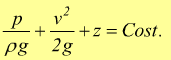
p=pressione
v=velocità
ρ=densità
g=accelerazione di gravità

Se prendiamo una condotta generica percorsa da un fluido che soddisfa
le caratteristiche a cui abbiamo accennato, il fluido nelle diverse
sezioni, possiede
• Energia di pressione.
• Energia cinetica.
• Energia potenziale.
![]() Energia
di pressione
Energia
di pressione
per la legge di Stevin 
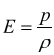 Energia
di pressione per unità di massa
Energia
di pressione per unità di massa
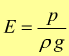 Energia
di pressione per unità di (forza) peso
Energia
di pressione per unità di (forza) peso
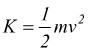 Energia
cinetica
Energia
cinetica  Energia
cinetica per unità di massa
Energia
cinetica per unità di massa
 Energia
cinetica per unità di peso
Energia
cinetica per unità di peso
![]() Energia
potenziale
Energia
potenziale ![]() Energia
potenziale per unità di massa
Energia
potenziale per unità di massa
![]() Energia
potenziale per unità di peso
Energia
potenziale per unità di peso
ma nell'equazione di Bernoulli convenzionalmente si usa la lettera z non la lettera h.
Come l'equazione di continuità, l'equazione di Bernoulli ha le caratteristiche di una legge di conservazione, per cui tra due sezioni S1 ed S2 del condotto che hanno altezze z1 e z2 rispetto ad un livello di riferimento convenzionale; deve valere il principio di conservazione dell'energia E1+K1+U1=E2+K2+U2 , quindi

Principio di Bernoulli: in un condotto percorso da un liquido perfetto in moto permanente, la somma delle energie di pressione, cinetica e potenziale resta costante in tutte le sezioni del condotto stesso.
Se chiamiamo H l'energia totale per unità di peso , fra le diverse forme di energia esiste la relazione

Se nell'equazione di Bernoulli portiamo tutti i termini al primo membro

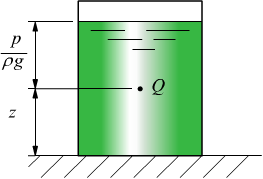
Se pensiamo ad un elemento Q, anche molto piccolo all'interno di un liquido, rivestono una certa importanza le due altezze:
![]() =
altezza piezometrica
=
altezza piezometrica
z=altezza geodetica
Se decidiamo di chiamare il termine 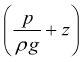 quota
piezometrica
quota
piezometrica
Sapendo che 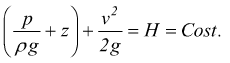
e che la velocita:
• diminuisce se il condotto è divergente
• aumenta se il condotto e convergente
• resta invariata se la sezione del condotto rimane costante
si deduce che la quota piezometrica 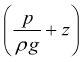
• aumenta se il condotto è divergente
• diminuisce se il condotto e convergente
• resta invariata se la sezione del condotto rimane costante
Questo ci permette di tracciare la linea piezometrica per un assegnato condotto.
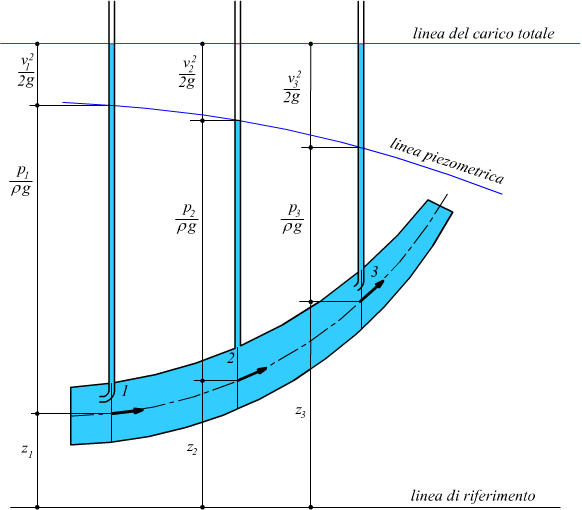
Dal disegno, la linea dell'energia totale appare costante come somma delle
tre energie specificate, questo è vero in condizioni di moto stazionario
ideale , ma nella realtà questa linea sarebbe progressivamente decrescente
a causa della presenza delle perdite di carico.
(N.B.: nel disegno è inserito un tubo di Pitot
per le sezioni 1 e 3 mentre è inserito un tubo piezometrico semplice
nella sezione 2)
La linea piezometrica, cioè la linea che unisce
tutte le quote piezometriche scende progressivamente, dato che la
sezione della condotta si restringe e la velocità aumenta.
In presenza di macchine operatrici (pompe, compressori) o motrici (turbine) la relazione di Bernoulli deve essere opportunamente modificata in:
![]()
H1=energia totale del liquido che entra nella sezione 1
w=energia equivalente al lavoro scambiato tra macchina e liquido
y=perdita di carico dovuta a dissipazione di energia
H2=energia totale del liquido che esce dalla sezione 2
Tutti questi termini rapresentano simultaneamente
delle energie specifiche ( o carichi ) e delle altezze, misurate in
metri di colonna d'acqua.
w è positivo se si tratta di un lavoro fatto da una macchina operatrice
che fornisce energia cinetica al fluido.
w è negativo se si tratta di un lavoro fatto da una macchina motrice
che utilizza l'energia cinetica del fluido.
| p1 | v1 [m/s] | z1 [m] |
| p2 | v2 [m/s] | z2 [m] |
| ρ [kg/m3] |
Teorema di Torricelli
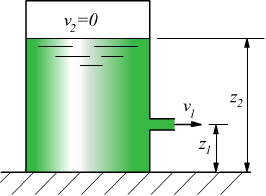
Una applicazione classica del principio di Bernoulli è quella che consiste nel calcolare la velocità di efflusso di un fluido da un rubinetto di un serbatoio.
A livello 2 e a livello 1 le pressioni sono uguali e pari alla pressione atmosferica.
Se la sezione del rubinetto è trascurabile rispetto a quella del serbatoio si può ammettere v2=0. L'equazione di Bernoulli diventa in tal caso
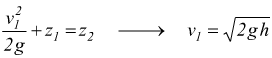
avendo posto z2-z1=h dislivello fra la superficie
libera del serbatoio e il rubinetto. Il risultato ottenuto è chiamato
teorema di Torricelli.
E' interessante notare come la velocità di efflusso è identica alla
velocità raggiunta da un corpo in caduta libera.
Tubo di Pitot

Lo strumento più comune per misurare la velocità di un liquido,
è il tubo di Pitot che assicura rilevamenti abbastanza precisi
sia nei corsi d'acqua che nelle condotte ed inoltre permette di
rilevare la velocità in un punto qualsiasi della sezione.
Esso è formato da un tubo di vetro aperto ai due estremi e piegato
a forma di L che viene immerso nella corrente.
Sia nel caso di fiumi o di canali, l'acqua per effetto della velocità
di cui è dotata salirà nel tratto verticale del tubo fino ad una
altezza h, misurata sopra il pelo libero
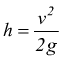
Inserendo il tubo di Pitot in una condotta la misurazione non è precisa se si trascura di applicare ad essa anche un tubo piezometrico. Nella tubazione, infatti, il liquido è sottoposto a pressione, e l'altezza rilevata col tubo di Pitot
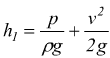
Il tubo piezometrico,da parte sua, è impossibilitato per la
sua conformazione a rilevare l'altezza cinetica.
Esso è solo rappresentativo di quanto prevale la pressione (relativa)
interna al fluido rispetto la pressione atmosferica e misura una quota
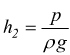 il
valore della velocità si ottiene quindi come:
il
valore della velocità si ottiene quindi come:
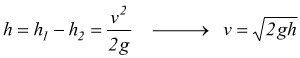
Venturimetro
Il tubo di Venturi costituisce un'applicazione del principio di Bernoulli, utilizzata in un dispositivo per misurare la portata dei fluidi in pressione entro condotti chiusi.
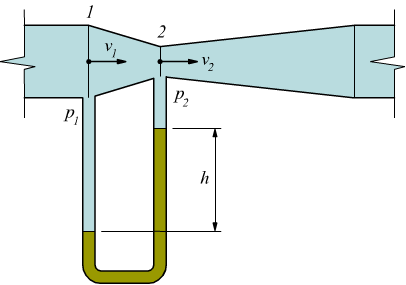
Il tubo di Venturi è formato da un primo tronco di cono convergente
da una sezione iniziale S1 ad una sezione finale S2
< S1.
Dalla strozzatura S2 parte un altro tronco di cono
divergente, detto diffusore.
Se si applica un manometro differenziale tra le sezioni S1
e S2, si rileva un dislivello h, che risulta
proporzionale alla portata del fluido nel condotto, secondo una
relazione che dipende dalle S1 e S2, dal
dislivello h e dalla densità del fluido.
Indichiamo con p1 e v1 i valori della pressione e della velocità nella sezione 1, posta all'imbocco dell'apparecchio, e p2 e v2 i valori della seconda sezione coincidente con quella di area minima; in seguito alla riduzione di sezione, la velocità aumenta v2>v1 e diminuisce di conseguenza la pressione p2< p1. Senza perdite di carico si ha:
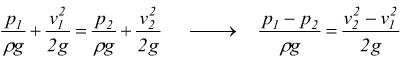
questo nell'ipotesi che l'apparecchio sia disposto ad asse orizzontale z1=z2.
Le pressioni p1 e p2 essendo poco diverse tra
loro non possono essere misurate da comuni manometri per questo esse
sono collegate tra loro da un manometro differenziale. Per effetto della
minore pressione esistente nella sezione 2, il liquido monometrico risalirà
nel relativo tubo creando tra i due rami del manometro un dislivello
h possiamo dunque scrivere Se indichiamo con
ρ=densità del liquido che scorre nella tubazione
ρ'=densità del liquido manometrico
![]()
divedendo membro a membro per ρg:
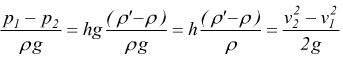 dato
che nella condotta il regime è stazionario:
dato
che nella condotta il regime è stazionario:
 m=S1/S2:
rapporto di strozzamento
m=S1/S2:
rapporto di strozzamento

si ha in definitiva 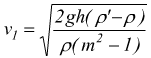
 edutecnica
edutecnica