Torsione
La torsione nei materiali è una deformazione che avviene quando un materiale viene sottoposto a una coppia di forze opposte che agiscono in senso rotatorio rispetto all'asse del materiale stesso. Questo tipo di deformazione provoca una torsione o una rotazione del materiale lungo la sua lunghezza.
In altre parole, si può dire che un solido è sollecitato a torsione, quando le sue sezioni trasversali, tendono a ruotare mutuamente, per effetto di due coppie di forze, uguali e contrarie che agiscono in piani normali rispetto all'asse longitudinale del solido, ad una certa distanza tra loro.
Per essere soggetto a torsione, su un solido, deve esercitarsi un momento torcente Mt agente nel piano perpendicolare all'asse del solido stesso.
La torsione può causare danni al materiale se non è adeguatamente progettato per resistere a questo tipo di stress. La torsione è comunemente osservata in materiali come metalli, legno e materiali compositi.
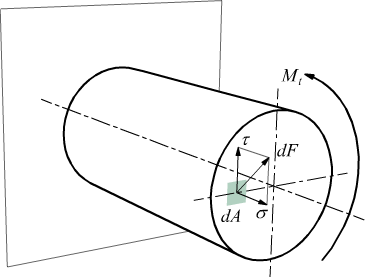
Ipotizziamo una trave a sezione circolare di raggio (r) e lunghezza
(l) incastrata ad un estremo.
Suddividiamo l'area A della sezione in tanti elementi (piccoli a piacere)
dA.
Ciascun elemento dA si troverà ad una distanza x rispetto all'asse della
trave.
La condizione di equilibrio tra il momento torcente applicato Mt
e le tensioni τ che si instaurano nelle aree elementari può esprimersi
come:
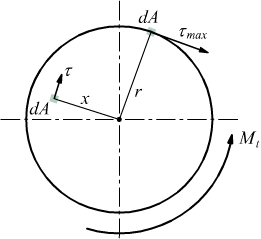
Se prendiamo due aree elementari dA poste una a distanza x e l'altra all'estremo r della sezione si può stabilire la proporzione
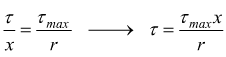sostituendo
nella precedente
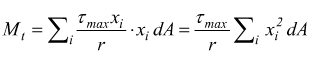
ma 
momento
d'inerzia polare della sezione rispetto all'asse della trave.
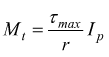viene
definito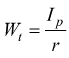 
modulo
di resistenza a torsione
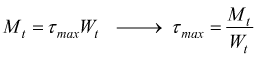
la condizione di resistenza a torsione è
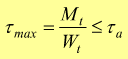con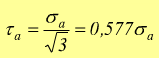 
tensione
tangenziale ammissibile
questo in condizioni statiche dove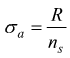 
con
ns=3÷5 ed R=carico unitario di rottura
in condizioni dinamiche si ha
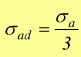e
va calcolato 
e
la condizione di resistenza a torsione diventa
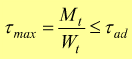
poi ricordando che
nel caso della sezione circolare piena: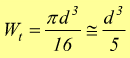 
nel caso della sezione circolare cava: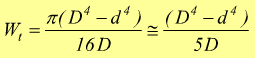 
con D= diametro maggiore e d=diametro minore.
Queste formule sono molto importanti per dimensionare un albero in condizioni di fatica. Altre formule ricorrenti, in questo caso, sono:
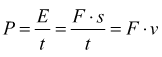
nel caso di un albero rotante v=velocità periferica 
con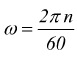 
quindi
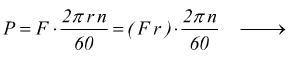
con P in [W] Mt in [Nm] ed ω in [rad/s]. La stessa formula può essere scritta come
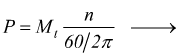
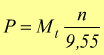
se teniamo la potenza in kW useremo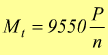 
mentre n è [g/min] ed Mt in [Nm].
Angolo di torsione
Come si può immaginare, nel caso della torsione, le tensioni massime si verificano alla periferia della sezione circolare, mentre al centro della stessa le tensioni sono nulle. Anche in questo caso si ha una deformazione elastica per la quale, la legge di Hooke può essere formulata come
con γ=scorrimento relativo (analogo all'allungamento relativo ε della trazione).
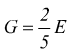modulo
di elasticità tangenziale; si ha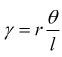 
con θ=angolo di torsione, l=lunghezza dell'albero ed r=raggio
della sezione.
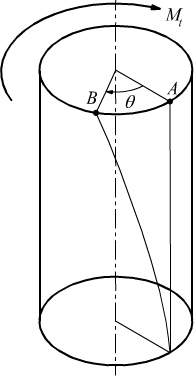
Un punto A all'estremità della sezione , sotto l'azione del momento
torcente Mt si sposta in B ruotando dell'angolo θ :
angolo di torsione. L'angolo di torsione θ si può calcolare come
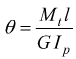
con Ip=momento polare di inerzia [mm4] rispetto
al centro della sezione.
Il prodotto G·Ip è chiamato rigidità torsionale.
A parità di momento torcente, una elevata rigidità torsionale
comporta un piccolo angolo di torsione.