Momento di inerzia
Il momento d'inerzia è una grandezza fisica che misura la resistenza di un oggetto a cambiare il suo moto rotazionale.
Si calcola rispetto all'asse di rotazione e dipende dalla distribuzione di massa dell'oggetto e dalla distanza dei suoi elementi di massa dall'asse.
Maggiore è il momento d'inerzia, maggiore sarà la resistenza dell'oggetto a cambiare la sua velocità di rotazione.
Momento di inerzia di una superficie
Ipotizziamo una generica superficie di area A e supponiamo che questa possa essere suddivisa in un grande numero di piccole aree elementari ai , ipotizziamo,inoltre, una retta r complanare con la superficie data.
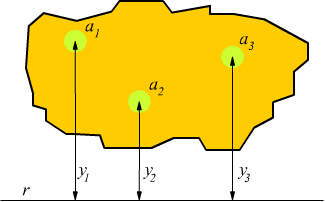
Viene definito momento di inerzia della superficie rispetto alla retta (r) assegnata, la sommatoria dei prodotti delle singole aree elementari ai per i quadrati delle rispettive distanze
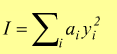 [m4 ]
[m4 ]
A differenza del momento statico che può assumere valori positivi, negativi o nulli, il momento di inerzia è una grandezza sempre positiva, perchè anche se le distanze yi possono assumere valori positivi o negativi rispetto alla retta (r) il loro quadrato è sempre positivo.
Teorema di trasposizione di Huygens
Consideriamo una superficie generica A di cui sia nota la posizione del baricentro G e si sia calcolato già in precedenza il momento di inerzia Ixo rispetto ad una retta xo passante per il baricentro.
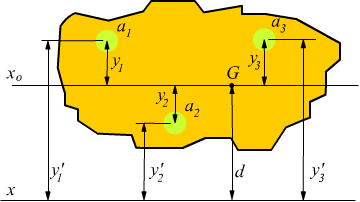
Se vogliamo ottenere il momento di inerzia Ix della superficie rispetto ad una retta x parallela ad xo e distante d da essa, si può dimostrare che è
![]()
Raggio di inerzia
Nel caso del momento di inerzia di una superficie non è più valido il teorema di Varignon ma vale una relazione analoga
![]()
dove il termine ρi non rappresenta la distanza della
retta x dal baricentro G della superficie ma la distanza fittizia della
retta dal punto in cui si dovrebbe concentrare tutta l'area A della
superficie per ottenere lo stesso momento di inerzia.
Il termine ρi [m] è denominato raggio
di inerzia.
Momento centrifugo di superficie
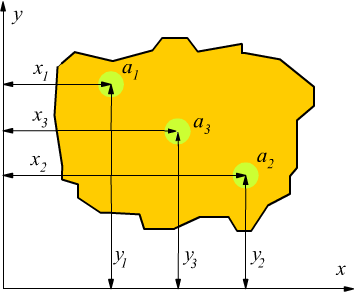
Viene definito momento centrifugo (o prodotto di inerzia) di una superficie rispetto a due rette qualsiasi x ed y, la somma dei prodotti delle singole aree elementari ai per le rispettive distanze dalle due rette.
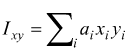 [m4 ]
[m4 ]
ha le stesse dimensioni del momento di inerzia, ma a differenza di esso può assumere valori negativi, positivi o nulli.
Momento polare di inerzia
Si definisce momento polare di inerzia di una superficie rispetto ad un punto P, complanare alla superficie, la sommatoria dei prodotti delle singole aree elementari ai per i quadrati delle rispettive distanze di dal punto P.
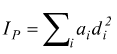 [m4 ]
[m4 ]
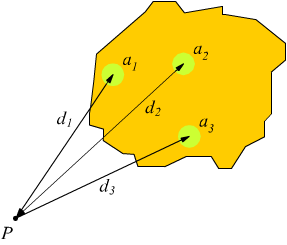
Se si imposta una coppia di assi cartesiani perpendicolari passanti per il punto P è possibile esprimere la generica distanza
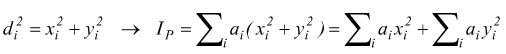
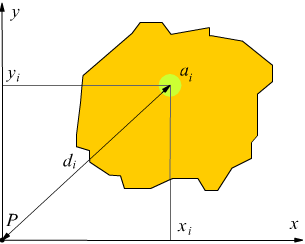 dunque:
dunque:
![]()
Il momento di inerzia polare IP rispetto ad un punto P è
uguale alla somma dei due momenti di inerzia assiali Ix e
Iy calcolati rispetto alle due rette perpendicolari passanti
per P.
Anche per il momento polare di inerzia è possibile applicare la formula
di trasposizione di Huygens
![]()
con Io momento polare rispetto al baricentro G e d distanza del baricentro dal punto P.
Momento di inerzia di un rettangolo
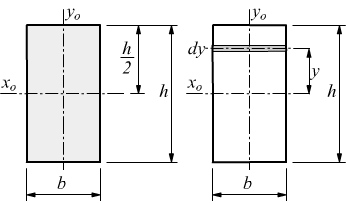
Per un rettangolo di base b ed altezza h il momento di inerzia rispetto all'asse baricentrico xo parallelo alla base è
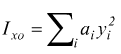
passando al calcolo differenziale possiamo pensare di porre l'area ai in termini infinitesimi come ai=b·dy
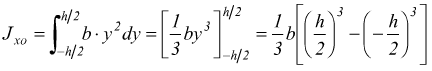
oppure ponendo l'area infinitesima ai=dx·dy usando gli integrali doppi:
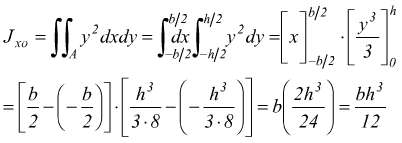
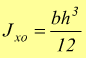
Se ci si riferisce all'asse verticale baricentrico yo basta pensare di ribaltare il rettangolo applicando ad esso lo stesso procedimento scambiando le due dimensioni b ed h, ottenendo
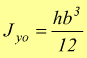
Ricordando che è ![]() il
momento polare di inerzia rispetto al baricentro G del rettangolo è
il
momento polare di inerzia rispetto al baricentro G del rettangolo è
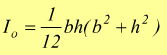
Momento di inerzia di un triangolo
Nel caso del triangolo le cose sono leggermente più complicate. Però abbiamo visto che per trovare il momento di inerzia di corpi bidimensionali si possono applicare gli integrali doppi ponendo ai=dxdy area infinitesima.
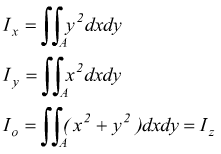
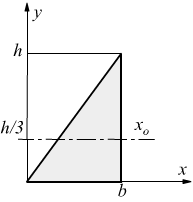
Per il triangolo qui disegnato vediamo che il dominio di integrazione è limitato superiormente dalla retta y=(h/b)·x di questo bisogna tener conto quando si impostano gli estremi di integrazione.
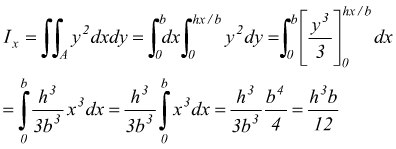
poi applichiamo il teorema di trasposizione sapendo che tra la base del triangolo e l'asse baricentrico vi è una distanza d=h/3.
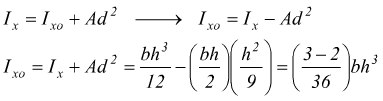
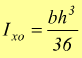
questa espressione è indipendente dalla forma del triangolo a patto (appunto) che b sia la base ed h l'altezza. In modo analogo si dimostra che
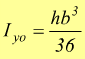 con
il momento polare rispetto al baricentro
con
il momento polare rispetto al baricentro
![]()
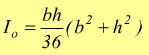
Momento di inerzia di un cerchio
Nel caso del cerchio di equazione
![]()
conviene usare le coordinate polari facendo coincidere l'origine del sistema di coordinate adottato con il centro della superficie del cerchio.
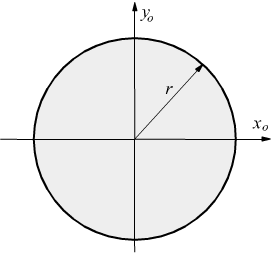
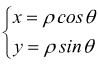
ricordando che negli integrali doppi la trasformazione da coordinate cartesiane a coordinate polari è
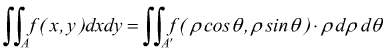
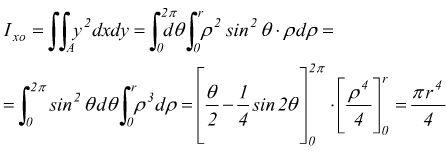
Per ragioni di simmetria deve essere
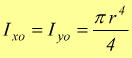 di
conseguenza il momento polare rispetto al baricentro
di
conseguenza il momento polare rispetto al baricentro
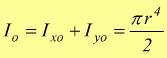
Momento di inerzia di una corona circolare
Per il momento di inerzia della corona circolare si può usare lo stesso approccio; chiaramente il suo momento di inerzia può essere ottenuto sottraendo il momento di inerzia del cerchio interno da quello del cerchio esterno
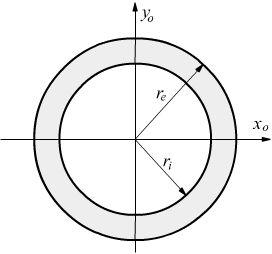
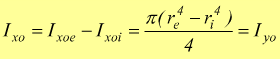 momento
polare rispetto agli assi baricentrici
momento
polare rispetto agli assi baricentrici
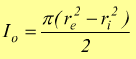 momento
polare rispetto al baricentro della figura
momento
polare rispetto al baricentro della figura
Per i seguenti profili composti, invece , vale la formula
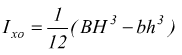
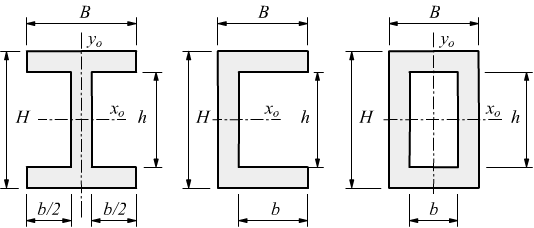
Energia cinetica nel moto rotatorio
Consideriamo una puleggia che ruota di moto circolare uniforme e immaginiamo di decomporla in tante particelle uguali di massa m1 m2 m distanti rispettivamente r1 r2 r dal centro di rotazione O.
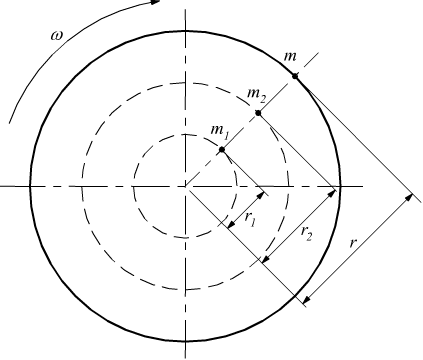
La particella m sulla periferia, ruota alla velocità periferica v della puleggia di raggio r.
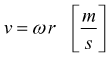 con
ω velocità angolare della puleggia
con
ω velocità angolare della puleggia
Adesso pensiamo al lavoro necessario per far acquistare ad ogni singola massa elementare una certa velocità v. Esso è pari a
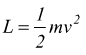
Il lavoro totale, sarà la somma di tanti lavori parziali
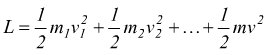 quindi
quindi
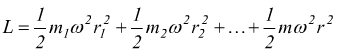 cioè
cioè
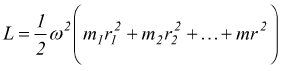
si definisce in questo modo il momento di inerzia di massa:
![]()
e si avrà 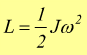
Si vede come la formula sia in stretta analogia con l'espressione dell'energia cinetica del moto traslatorio, dove il lavoro svolto è formalmente
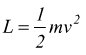
con la differenza che al posto della velocità di traslazione viene sostituita la velocità angolare e la massa viene sostituita dal momento di inerzia.
Il momento di inerzia di massa è, dunque, strettamente legato alla eventualità che un corpo rigido possa ruotare; esso rappresenta la reazione di inerzia che il corpo oppone alle forze che tendono a farlo ruotare attorno ad un determinato asse.
Momenti d'inerzia assiali di massa
Il momento di inerzia ora calcolato si riferisce all'asse di rotazione della puleggia che poi coincide con il baricentro della puleggia stessa, non sempre l'asse di rotazione di un corpo rigido passa per il suo baricentro dunque più in generale:
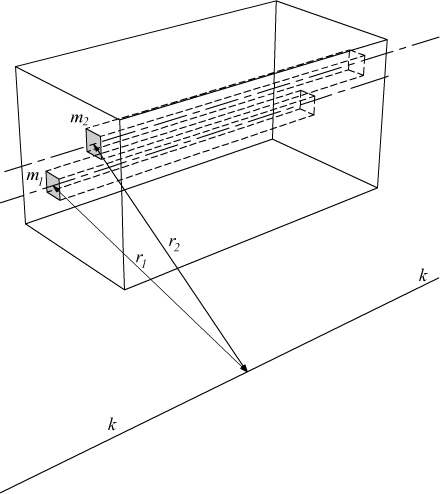
Si definisce momento
d'inerzia assiale di massa J di un solido, rispetto ad una retta k prefissata,
la sommatoria dei prodotti delle singole masse elementari mi
per i quadrati delle rispettive distanze ri valutate
dal centro delle masse alla retta r.
In forma analitica:
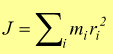 [
kg·m2 ]
[
kg·m2 ]
Per i momenti di inerzia assiali di massa valgono le stesse proprietà già viste per i momenti di inerzia delle superfici.
• Il momento d'inerzia di massa è una grandezza che assume il valore minimo quando è calcolato rispetto a un asse baricentrico;
• Noto il momento d'inerzia di massa rispetto a un asse baricentrico xo si può valutare il momento rispetto a un altro asse x parallelo a xo posto a distanza d dal primo, con formula di trasposizione:
![]()
La nozione di raggio di inerzia ( o raggio giratore ) è presente anche nella definizione del momento di inerzia di massa
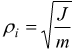
Noto il raggio d'inerzia ρ il momento d'inerzia si ottiene moltiplicando la massa totale m del corpo per il quadrato del raggio d'inerzia stesso:
![]()
Questa semplice regola pratica consente il calcolo del momento d'inerzia
di massa di qualsiasi solido cilindrico o prismatico (a sezione costante)
rispetto al proprio asse geometrico.
Non si può operare allo stesso modo sui solidi di tipo diverso (per
esempio,cono o piramide), non essendo costante la sezione nei diversi
punti dell'asse.
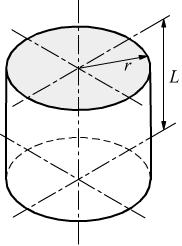
Momento di inerzia di un cilindro
 I
corpi cilindrici ruotano quasi sempre intorno al loro asse geometrico
;dobbiamo perciò calcolare il momento d'inerzia di massa di un cilindro
rispetto a quell'asse.
I
corpi cilindrici ruotano quasi sempre intorno al loro asse geometrico
;dobbiamo perciò calcolare il momento d'inerzia di massa di un cilindro
rispetto a quell'asse.
Si ricava il raggio di inerzia ρi dal momento polare di superficie riferito al centro di una sezione normale all'asse geometrico e poi si moltiplica il suo quadrato per per la massa m del cilindro.
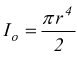
dividiamo per l'area del cerchio A:
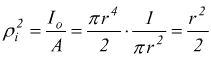
ottenendo poi il momento di inerzia rispetto all'asse di rotazione
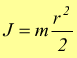
Momento di inerzia di un prisma retto a sezione quadrata
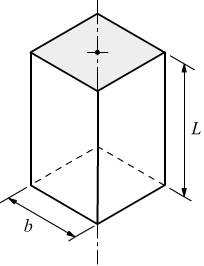 Se,
ad sempio,consideriamo un prisma retto di lunghezza L, a sezione quadrata
e di lato b, il momento d'inerzia baricentrico rispetto al centro della
sezione è :
Se,
ad sempio,consideriamo un prisma retto di lunghezza L, a sezione quadrata
e di lato b, il momento d'inerzia baricentrico rispetto al centro della
sezione è :
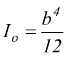
si ha
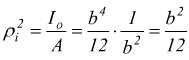
di conseguenza il momento di inerzia di massa rispetto al suo asse longitudinale
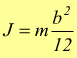
Momento di inerzia di un cilindro cavo
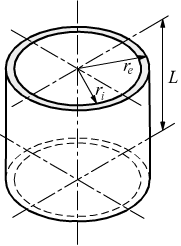 Nel caso del
cilindro cavo la sezione normale all'asse geometrico è una corona circolare
di raggi re (esterno) e ri (interno), il momento
d'inerzia polare rispetto al centro di tale corona ha l'espressione:
Nel caso del
cilindro cavo la sezione normale all'asse geometrico è una corona circolare
di raggi re (esterno) e ri (interno), il momento
d'inerzia polare rispetto al centro di tale corona ha l'espressione:
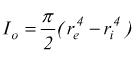
che può essere posta anche sotto la forma:
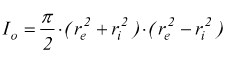
dividiamo per l'area A
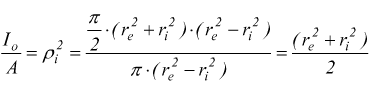
quindi il momento d'inerzia di massa I rispetto all'asse geometrico longitudinale vale:
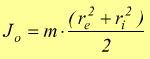
Riportiamo di seguito alcuni momenti di inerzia di uso comune
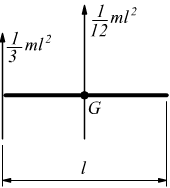 asta
omogenea
asta
omogenea
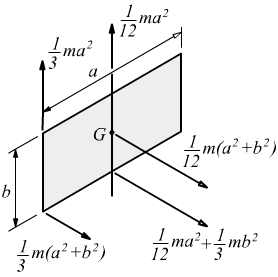 lamina
rettangolare omogenea
lamina
rettangolare omogenea
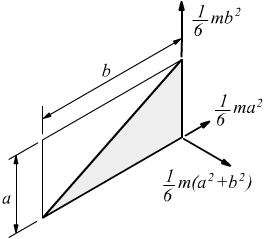 triangolo
rettangolo omogeneo
triangolo
rettangolo omogeneo
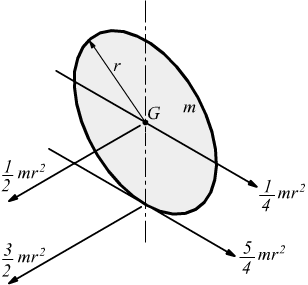 disco
omogeneo
disco
omogeneo
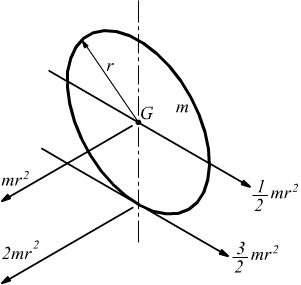 circonferenza
omogenea
circonferenza
omogenea
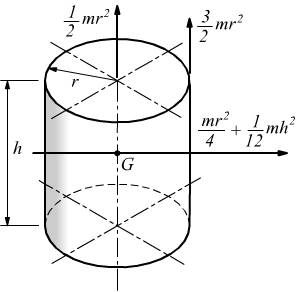 cilindro
omogeneo
cilindro
omogeneo
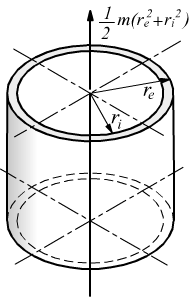 cilindro
cavo omogeneo
cilindro
cavo omogeneo
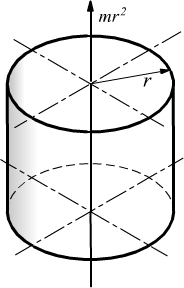 cilindro
cavo omogeneo di spessore trascurabile
cilindro
cavo omogeneo di spessore trascurabile
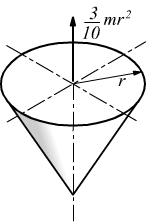 cono
omogeneo
cono
omogeneo
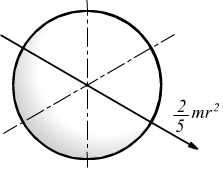 sfera
omogenea
sfera
omogenea
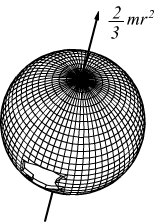 sfera
cava
sfera
cava
 edutecnica
edutecnica