Moto armonico

     

Qualsiasi movimento che si ripeta ad intervalli regolari è chiamato moto periodico. Il moto armonico semplice è una forma di moto periodico che ha la caratteristica di poter essere ricondotto alla proiezione lungo un asse di una particella che si muove di moto circolare uniforme.

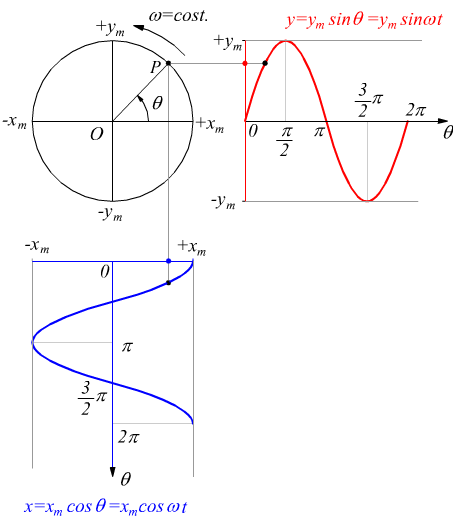
immaginiamo di proiettare la posizione della particella P, rotante lungo la circonferenza di centro O, sull'asse orizzontale x, osserveremo la proiezione oscillare avanti e indietro di una ugual distanza x_m a destra e a sinistra rispetto all'origine. Il valore x_m (-x_m) rappresenta, dunque, il valore massimo (minimo) dell’elongazione lungo l’asse x (ampiezza).

Se il punto materiale che percorre la circonferenza esegue un giro completo in un tempo T, allora T viene chiamato periodo, mentre f=1/T viene chiamata frequenza e definisce il numero di giri che la particella esegue in un secondo.

Per percorrere un giro completo la particella deve coprire un angolo θ=2π in un tempo di T secondi con velocità angolare

    

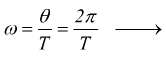
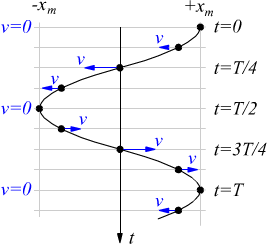
Se si volesse rilevare la posizione e la velocità della particella proiettata lungo l'asse x al passare del tempo avremmo una situazione che può essere compendiata del seguente disegno

.

Come si vede il punto mobile lungo l’asse orizzontale x ha velocità massima nel punto x=0 e velocità nulla nei punti x=±x_m.
Si tratta dunque di un moto accelerato.
La legge oraria che definisce la posizione lungo l'asse x sarà

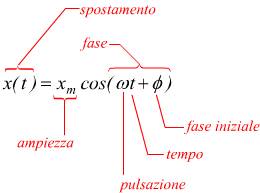
è facile dedurre questa legge se immaginiamo che all'istante iniziale la fase sia ϕ=0.
In un generico istante successivo la particella avrà coperto un arco di circonferenza θ al tempo t=0:

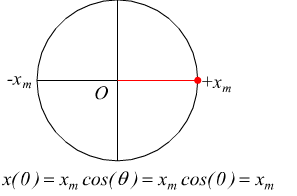
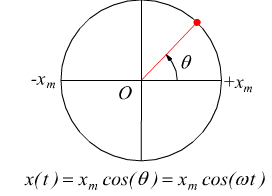
quindi, se la fase iniziale ϕ=0, essendo θ=ωt, si ha:

Velocità nel moto armonico

     

Formalmente, in Fisica, la velocità si ottiene eseguendo la derivata rispetto al tempo dello spostamento (spazio).

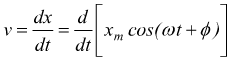    si ha

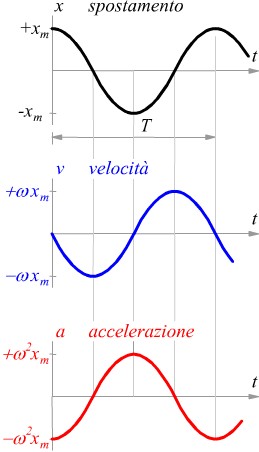
Supponendo per semplicità ϕ=0 confrontando i grafici di spostamento e velocità, facciamo, ancora una volta, notare come la velocità si annulla nei punti di massimo e minimo dell'elongazione (spostamento) rispetto all'origine O (x=x_m oppure x=-x_m); mentre la velocità è massima ogni volta che la proiezione della particella passa per l'origine x=0.

Accelerazione nel moto armonico

     

Formalmente l'accelerazione si ottiene derivando la velocità rispetto al tempo.

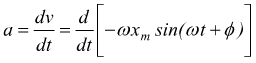     pertanto, si ha

Sempre osservando i grafici di spazio tempo e velocità si nota come l'accelerazione si annulla ed inverte il suo segno per x=0, in valore assoluto, l'accelerazione è massima nei punti di massima elongazione x = x_m oppure x = –x_m.

Legge di Hooke

          

Se è nota l'accelerazione di un corpo di massa m che si muove di moto armonico, allora è possibile individuare la forza F che provoca tale moto; infatti dalle precedenti equazioni risulta:

    

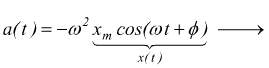
La seconda legge della dinamica afferma che

           1

k=mω² viene chiamata costante elastica.
Mentre le relazioni precedenti esprimevano il moto armonico semplice dal punto di vista cinematico, l'equazione 1 esprime il moto armonico semplice dal punto di vista della dinamica.

Dal punto di vista dinamico il moto armonico semplice è il movimento di una particella di massa m, soggetta ad una forza proporzionale allo spostamento della particella ma di segno opposto.

Nella legge di Hooke si riconosce come in questo tipo di moto la forza è sempre opposta e proporzionale allo spostamento.

L'equazione 1 riscrivibile come

è un'equazione differenziale lineare omogenea del secondo ordine a coefficienti costanti la cui equazione caratteristica è:

essa ha due radici complesse coniugate immaginarie pure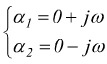

e ammette la soluzione generale

per la velocità si vede come sia

mentre per l'accelerazione

per t=0 poniamo x=x_m ed x'=0 si ha 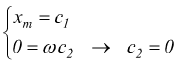   per cui si ottiene

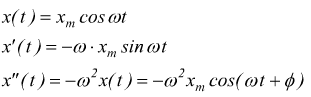
Le relazioni notevoli che si possono dedurre dalla legge di Hooke sono:

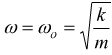          pulsazione naturale[ rad/s ]

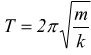     periodo [ s ]

   ampiezza [m]

   fase iniziale [rad]

Oscillatore armonico

     

Tutte le regole precedenti sono caratteristiche che contraddistinguono un sistema fisico chiamato oscillatore armonico lineare che consiste nell'apparato massa-molla qui sotto schematizzato.

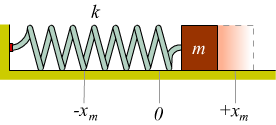
Questo sistema, dove si sottintende gli attriti siano trascurabili, inizia ad oscillare quando la massa viene tirata lateralmente e poi lasciata libera di muoversi.
Questo sistema rispetta tutte le leggi del moto armonico semplice, a partire dal fatto che la forza F che si esercita sulla massa è sempre opposta allo spostamento di questa.

Tutti i sistemi oscillanti sono regolati da queste leggi, fra i principali sistemi che rispettano queste leggi sono la molla e il pendolo.

Moto armonico smorzato

     

Si può intuire che il sistema massa-molla appena visto, può continuare ad oscillare indefinitivamente solo in condizioni ideali, cioè, in assenza di qualsiasi attrito con la superficie di contatto, ma anche la presenza di eventuali fluidi come aria od acqua comportano una condizione di progressivo smorzamento del moto oscillante. Un oscillatore armonico può essere descritto dal seguente schema:

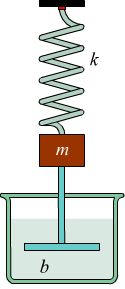
dove al sistema massa-molla viene collegata una paletta (idealmente priva di massa) immersa nell'acqua.
Oscillando assieme alla massa m, la paletta immersa nel liquido, eserciterà una forza frenante che chiamiamo R = – bv proporzionale alla velocità istantanea della paletta nel fluido.

In tal caso la legge di Hooke deve essere corretta per far fronte all'attrito viscoso

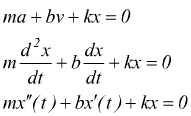
si ottiene l'equazione caratteristica

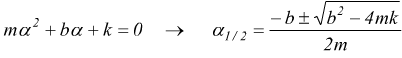
che dipende da come si comporta il discriminante di questa equazione di secondo grado:

  si ha moto sovrasmorzato le radici sono reali e distinte e la soluzione generale è:

Le due radici α₁ ed α₂ sono negative dunque x → 0 per t → ∞.

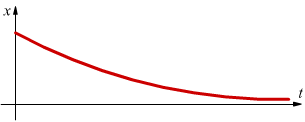
moto criticamente smorzato: in questo caso l'equazione caratteristica ha radici reali coincidenti:

  moto criticamente smorzato: in questo caso l'equazione caratteristica ha radici reali coincidenti :

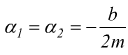   la soluzione diventa

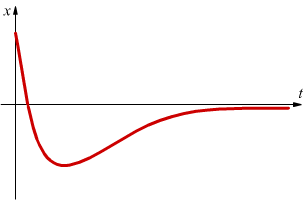
la risposta è simile al caso precedente, lo smorzamento è ancora in grado di evitare le oscillazioni .

  moto debolmente smorzato : in questo caso le radici sono complesse coniugate

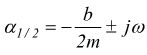   con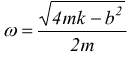   

la soluzione generale è la seguente

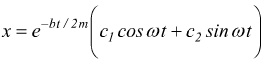
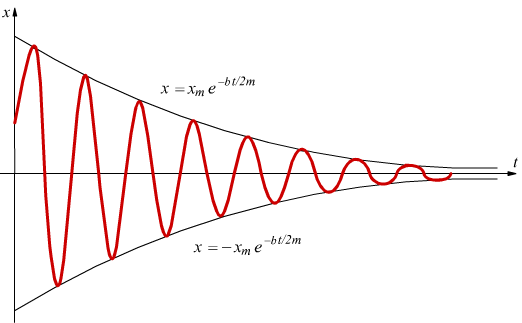
anche in questo caso si ha x → 0 per t → ∞ ma c'è anche la presenza di oscillazioni inviluppate in una curva esponenziale decrescente.
Imponendo le precedenti condizioni al contorno si ottiene :

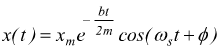
con ω_s= pulsazione dell'oscillatore smorzato

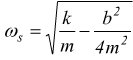
se b=0 e si ha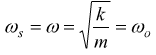

D'ora in poi col temine ω_o intendiamo la pulsazione naturale del sistema molla-massa in assenza di smorzamento, che attenuerebbero le oscillazioni, ma anche in assenza di forza che ne incentiverebbero le oscillazioni (oscillazioni forzate). I valori che rappresentano ω_s sono tutti costanti, ragion per cui questo tipo di moto è caratterizzato da una frequenza (e quindi un periodo T) costanti, ma l'ampiezza è variabile.

E' evidente che se non ci sono attriti (smorzamento) o cause forzanti che provocherebbero oscillazioni il sistema molla-massa continuerebbe ad oscillare autonomamente alla stessa pulsazione ω_o in definitivamente (fino alla fine dei secoli). Quindi in assenza di smorzamento, l'eq. precedente si riduce alla

Oscillazioni forzate

     

Possiamo ora pensare di immette energia nel sistema ad una certa frequenza, non necessariamente uguale alla frequenza (pulsazione) naturale del sistema.
Un esempio di oscillatore forzato potrebbe ad esempio essere una pallina di massa m, supportata da un elastico che leghiamo ad un nostro dito dall'altro suo estremo libero.

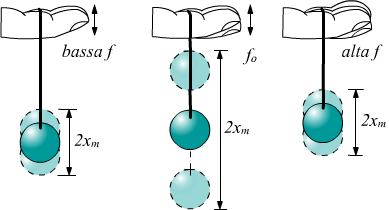
All'inizio, muovendo il dito lentamente, la palla rimbalza su e giù con una piccola quantità di smorzamento. Man mano che si aumenta la frequenza con cui muoviamo il dito su e giù, la pallina risponde oscillando con ampiezza crescente. Quando il moto alternativo del dito viene portato verso la frequenza naturale, le oscillazioni della pallina aumentano di ampiezza ad ogni oscillazione. Il fenomeno della guida di un sistema ad una frequenza uguale alla sua frequenza naturale si chiama risonanza.

Un sistema forzato a vibrare alla sua frequenza naturale si dice in risonanza. Man mano che la frequenza di guida diventa progressivamente superiore alla frequenza di risonanza o naturale, l'ampiezza delle oscillazioni si riduce fino a quando le oscillazioni pressoché scompaiono e il dito si muove semplicemente su e giù con scarso effetto sulla pallina.

Si intuisce che a frequenze forzate più alte e più basse, l'energia viene trasferita alla pallina in modo meno efficiente e risponde con oscillazioni di ampiezza inferiore.

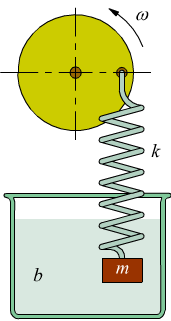
Se volessimo progettare un meccanismo per conferire oscillazioni forzate ad un sistema smorzato potremmo collegare una massa m immersa in un fluido viscoso, ad una molla simile all'apparato discusso nell'oscillatore armonico smorzato. Questa volta, invece di fissare l'estremità libera della molla ad un vincolo fisso, possiamo collegare l'estremità libera a un disco azionato da un motore a velocità variabile. Il motore gira con una frequenza angolare di azionamento di Ω . Il disco rotante fornisce energia di lavoro al sistema con forza motrice pari a F(t)=F_ocos(Ωt). L'equazione verrebbe modificata come:

  

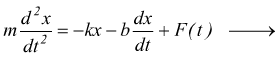
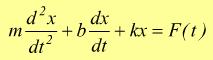
ponendo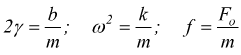

integrando quest'ultima equazione differenziale, si ottiene la soluzione particolare

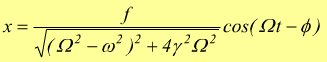     2

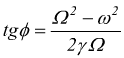con    3

mentre chiamiamo ampiezza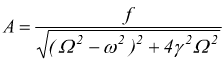      

questa appena trovata, viene anche chiamata soluzione stazionaria. Le oscillazioni che hanno luogo, chiamate anche oscillazioni forzate, hanno frequenza uguale alla frequenza della forzante applicata ma sono in ritardo rispetto ad essa di un angolo di fase pari a ϕ.

Nel seguente disegno viene dato il grafico dell'ampiezza A in funzione della pulsazione forzante Ω per un dato valore di del fattore di smorzamento b. L'ampiezza ha un massimo pronunciato quando il denominatore dell'eq. 2 è minimo.

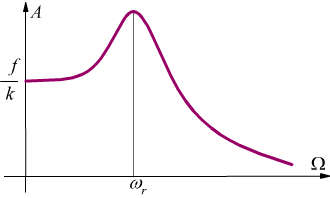
Ciò si verifica per 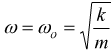   alla frequenza ω_r data dalla

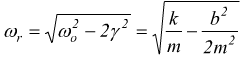
Quando la pulsazione della forzante Ω = ω_r si dice che il sistema è in risonanza di ampiezza. Quanto minore è lo smorzamento tanto più pronunciata è la risonanza. Quando lo smorzamento b è nullo, la risonanza ha ampiezza infinita e ha luogo per

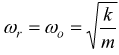
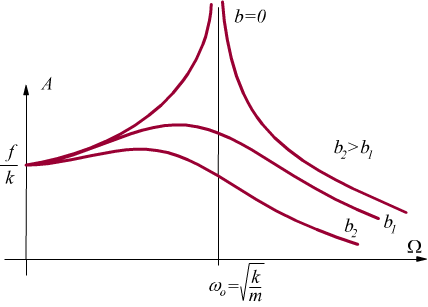
nel seguente grafico viene mostrata la variazione di ampiezza A dell'oscillazione in funzione della frequenza forzante Ω per differenti valori dello smorzamento b.

La velocità dell'oscillatore forzato si può ottenere come

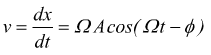
Confrontando questa espressione con quella della forza F(t)=F·cos(Ωt) vediamo che ϕ rappresenta lo spostamento di fase della velocità rispetto alla forza applicata. L'ampiezza della velocità vale

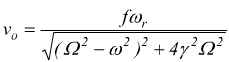    che si può anche scrivere come

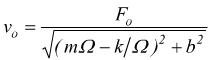
Il valore di v_o varia con con Ω come si vede dal grafico sotto

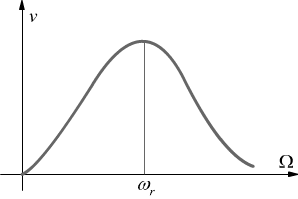
e raggiunge il massimo quando la quantità tra parentesi al denominatore dell'eq. precedente è nulla, quando la pulsazione della forzante è uguale alla pulsazione naturale del sistema privo di attrito.

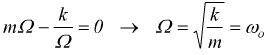    4

Per questa frequenza della forza applicata, la velocità e l'energia cinetica dell'oscillatore sono massime , in tal caso si dice che si ha risonanza di energia. Sostituendo l'eq. 4 nell'eq. 3 con ω=ω_o si ottiene ϕ=0.
La risonanza di energia ha luogo quando la pulsazione della forza applicata è uguale alla pulsazione naturale dell'oscillatore senza smorzamento.. In questo caso la velocità è in fase con la forza applicata.
Queste sono le condizioni più favorevoli per il trasferimento di energia all'oscillatore.

Dato che la potenza trasferita all'oscillatore dalla forza applicata P=Fv e quenta quantità è sempre positiva quando F e v sono in fase, possiamo dire che all'energia di risonanza il trasferimento di energia dalla forza applicata all'oscillatore è massima.

La risonanza, si presenta praticamente in tutti i settori della fisica. Essa si verifica ogni volta che un sistema è soggetto ad un'azione esterna, che varia periodicamente nel tempo. Ad esempio se un gas è posto in una regione in cui esiste un campo elettrico oscillante (come in un'onda elettromagnetica) delle oscillazioni forzate vengono indotte negli atomi che compongono le molecole del gas. Poiché anche le molecole hanno una pulsazione naturale ben definita, l'assorbimento di energia è massimo quando la frequenza del campo elettrico applicato coincide la pulsazione naturale delle molecole. Applicando questo principio possiamo ottenere lo spettro vibrazionale delle molecole. Analogamente possiamo considerare gli elettroni di un atomo come oscillatori dotati di certe frequenze naturali. L'energia che un atomo assorbe da un campo elettrico oscillante è massima quando coincide con la frequenza naturale di quell atomo. Alcuni cristalli come il cloruro di sodio, sono composti da particelle cariche positivamente e negativamente (ioni). Se il cristallo è soggetto ad un campo elettrico oscillante esterno, gli ioni positivi oscillano rispetto a quelli negativi. L'assorbimento di energia da parte del cristallo è massimo quando la frequenza del campo elettrico coincide con la frequenza naturale di oscillazione degli ioni che nel caso del cloruro di sodio è pari 5×10¹² Hz. L'esempio più famigliare di risonanza è quello che si verifica quando sintonizziamo la radio su una stazione trasmittente. Tutte le stazioni trasmittenti producono oscillazioni forzate nel circuito ricevitore in ogni istante. Ma ad ogni posizione della sintonia corrisponde una frequenza naturale di oscillazione del circuito elettrico del ricevitore. Quando questa frequenza coincide con quella di una stazione trasmittente l'assorbimento di energia è massimo, e quindi questa è la sola stazione che si ascolta. Se due stazioni hanno frequenze di trasmissione molto vicine, talvolta le udiamo contemporaneamente, il che da luogo ad un effetto di interferenza .