Lavoro ed energia
Il lavoro in fisica è descritto come la quantità di energia trasferita da una forza applicata su un corpo in movimento.
Il lavoro, è dunque definito come il prodotto della forza applicata su un corpo e della distanza percorsa dal corpo nella direzione della forza.
Il lavoro è strettamente correlato all'energia in quanto il lavoro svolto su un corpo può determinare un aumento o una diminuzione dell'energia cinetica del corpo stesso. Ad esempio, se una forza applicata su un corpo in movimento agisce nella stessa direzione del moto, il lavoro svolto sarà positivo e aumenterà l'energia cinetica del corpo.
Al contrario, se la forza agisce in direzione opposta al moto, il lavoro svolto sarà negativo e ridurrà l'energia cinetica del corpo. Inoltre, il lavoro può anche essere convertito in altre forme di energia, come l' energia potenziale gravitazionale o l'energia termica. Ad esempio, il lavoro svolto sollevando un oggetto contro la forza di gravità aumenta l'energia potenziale gravitazionale dell'oggetto.
Si conclude che il lavoro è una misura della quantità di energia trasferita da una forza applicata su un corpo in movimento ed è strettamente correlato con l'energia cinetica, l'energia potenziale e altre forme di energia.
Lavoro
Quando su un corpo di massa m agisce una forza F di direzione ed intensità costanti, questo corpo subisce uno spostamento s.
Il lavoro di una forza F è definito come il prodotto dell'intensità della componente della forza, calcolata nella direzione dello spostamento, per lo spostamento del suo punto di applicazione.
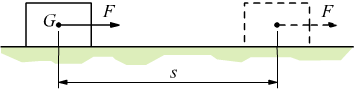
In forma analitica viene espresso dal prodotto scalare tra il vettore F e lo spostamento s che sono due grandezze vettoriali
![]() [
J ]
[
J ]
dove θ è l'angolo formato tra i vettori F ed s.
Il lavoro è sempre energia in fase di trasferimento.
L'energia può essere trasferita a un corpo, o da un corpo, per mezzo di
una forza che agisce su di esso.
● Quando l'energia è trasferita al corpo
il lavoro è positivo.
● Quando l'energia viene ceduta dal corpo
il lavoro è negativo.
Come si è specificato, il lavoro è una
grandezza scalare e la sua unità di misura è il joule.
Il joule è il lavoro compiuto da una forza di un newton quando il suo punto
di applicazione si sposta di un metro nella direzione e nel verso della
forza.
Se la forza F ha una direzione diversa rispetto a quella in cui è possibile
realizzare il moto, allora bisogna decomporre F e considerare solo la componente
che ha la stessa direzione del moto.
Nel seguente disegno si vede che la forza F forma col piano di appoggio
un angolo θ mentre il corpo può spostarsi solo in direzione dell'asse
positivo della x.
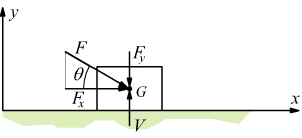
Decomponiamo la F nelle due direzioni ortogonali x ed y.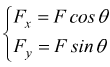
La Fy viene equilibrata dalla reazione vincolare del piano assieme alla forza peso (nel disegno non rappresentata) queste forze non possono produrre dunque nessuno spostamento. La componente Fx parallela al piano, provoca invece il moto del corpo e dunque compie il lavoro
![]()
Se la forza motrice F fosse stata parallela al piano, cosθ=cos0°=1 ed avremmo semplicemente avuto
![]()
Il vettore peso, invece, potrebbe compiere lavoro solo nell'ipotesi che sia in grado di produrre moto in direzione verticale, come nel caso di un corpo che cade per gravità.
Nel seguente schema, trascinando la punta del vettore F (verde) e la punta del vettore s (rosso) si vede come viene ottenuta la componente che qui chiamiamo (impropriamente) Fx disegnata in viola che sarebbe la componente del vettore F nella direzione dello spostamento: il lavoro viene calcolato come L=F·s·cosθ =Fx·s.
Se al corpo è applicata anche una forza resistente R ad esempio dovuta all'attrito con
![]()
con f=coefficiente di attrito e p=mg=peso del corpo.
La forza resistente va considerata, infatti nell'ipotesi che sia F>R
la forza che produrrà lo spostamento e quindi il lavoro sarà F-R, che
è come dire che F produce un lavoro positivo ed R un lavoro negativo.
Si definisce lavoro motore (positivo)
quello compiuto dalla forza motrice F , lavoro
resistente (negativo) quello compiuto dalla forza resistente
R.
In un moto di traslazione il lavoro motore uguaglia (almeno) il lavoro
resistente, o meglio
Lm=Lr moto uniforme
Lm>Lr moto uniformemente accelerato
Lm<Lr moto uniformemente decelerato
Essendo il lavoro, ottenuto da una operazione di prodotto scalare, fissata una coppia di coordinate cartesiane x,y in concomitanza del punto di applicazione della forza, possiamo avvalerci della regola
![]()
dove Fx Fy sx ed sy sono le componenti dei vettori F ed s lungo gli assi coordinati.Si tratta di una formula ottenuta dalla regola generale del prodotto scalare tra due vettori collocati su un piano cartesiano di coordinate xy.
![]()
Anche in questo caso occorre trascinare la punta dei due vettori per cambiarne modulo e direzione.
Energia cinetica
Supponiamo che su un corpo inizialmente fermo agisca una forza per
un dato intervallo di tempo t.
Sappiamo che il moto sarà accelerato con leggi
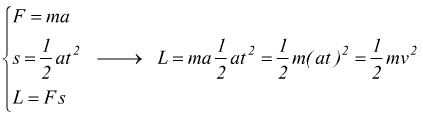
Il lavoro compiuto dalla forza si trasforma nell'energia cinetica
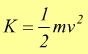 [
J ] dato che m=cost.
[
J ] dato che m=cost. 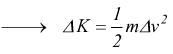
Teorema delle forze vive: il lavoro compiuto da una forza applicata ad un corpo è uguale alla variazione di energia cinetica del corpo stesso .
La variazione di energia cinetica di un corpo è dovuta alla variazione di velocità.
Come si è potuto notare, il lavoro è misurato in joule come l'energia (energia cinetica) più in generale, si può dire che l'energia è la capacità di un sistema fisico di compiere un lavoro. Questa capacità, implica in ogni caso, la presenza di una forza in grado di eseguire uno spostamento, dato che soltanto il prodotto tra queste due grandezze può generare il lavoro meccanico.
Teorema dell'energia cinetica+
Se un corpo possiede una energia cinetica iniziale e su di esso agisce
una forza che effettua un lavoro.
L'energia cinetica finale è uguale alla somma dell'energia cinetica iniziale
e del lavoro conferito.
![]()
in questa uguaglianza consiste il teorema dell'energia cinetica, dove:
Ki=energia cinetica iniziale del corpo
Kf=energia cinetica finale del corpo
Lavoro della forza gravitazionale
Il lavoro Lg svolto dalla forza di gravità Fg=mg agente sulla massa di un corpo è dato dalla relazione
![]()
con θ angolo tra i vettori Fg ed s.
Lavoro svolto nel sollevamento di un corpo
Il lavoro La effettuato da una forza nel sollevamento o nell'abbassamento di un corpo è in relazione al lavoro svolto dalla forza di gravità Lg sul corpo stesso dalla relazione
![]()
se l'energia cinetica iniziale e finale sono uguali si ha:
![]()
in pratica, la forza applicata trasferisce tanta energia al corpo quanta ne viene sottratta dalla gravità.
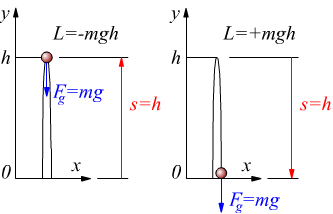
ricordiamo che il lavoro eseguito dal campo gravitazionale su una massa
in fase di salita è negativo e vale
![]()
ma come si vede dal disegno i vettori Fg ed s hanno verso contrapposto per cui cosθ=-1. Si deduce che il lavoro che deve essere eseguito sulla palla per alzarla dal livello y=0 al livello y=h è pari a
![]()
la palla ha infatti velocità iniziale e finale (al livello y=h) nulle.
Lavoro della forza elastica
La forza F esercitata da una molla è data dalla legge di Hooke
![]()
dove d è lo spostamento dell'estremità libera della molla rispetto la sua
posizione di riposo (non compressa e non allungata) con k costante elastica
[N/m].
Ad esempio, se facciamo uno spostamento d partendo dalla posizione di riposo
di una molla, allo spostamento si opporrà la forza F della molla in fase
di compressione che è diretta come si vede dal disegno in senso contrario
allo spostamento (cosθ=cos180°=-1).
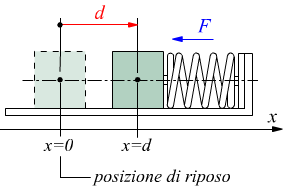
Se la forza e lo spostamento si svolgono lungo un unico asse che per comodità chiamiamo x, l'espressione precedente può essere scritta in forma scalare
![]()
bisogna dunque tener conto che la forza di una molla è non è costante ma variabile in funzione dello spostamento x.
Se un oggetto è fissato all'estremità libera di una molla, il lavoro Le compiuto dalla forza elastica della molla sull'oggetto, quando questo viene spostato dalla posizione iniziale xi alla posizione finale xf è dato dalla formula:
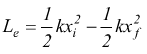
se xi=0 ed xf=x la formula diventa
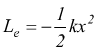
queste ultime osservazioni sono state già messe in evidenza nella pagina sull'energia potenziale della molla.
Lavoro svolto da una forza variabile
Quando la forza F agente su un oggetto, dipende dalla posizione dell'oggetto in uno spazio tridimensionale descritto dalle coordinate xyz, nell'ipotesi che la componente Fx dipenda esclusivamente da x, Fy dipenda esclusivamente da y ed Fz dipenda solo dalla coordinata z; il lavoro fatto sull'oggetto nel corso del suo spostamento da una posizione iniziale ri(xi,yi,zi) ad una posizione finale rf(xf,yf,zf) è dato dalla formula:
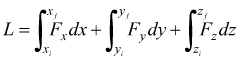
Principio di conservazione dell'energia
Questo principio può essere espresso nel modo seguente : la somma dell'energia potenziale e dell'energia cinetica possedute da un corpo è costante.
![]() o
anche
o
anche ![]()
Ui=energia potenziale iniziale
Ki=energia cinetica iniziale
Uf=energia potenziale finale
Kf=energia cinetica finale
ET=energia totale
Il principio è puramente teorico si riferisce ad un sistema isolato dove siano presenti solo forze conservative.
Lavoro di una coppia
Prendiamo un corpo per semplicità cilindrico inizialmente fermo ipotizzando che ruoti attorno al proprio asse sotto l'effetto di una forza periferica F percorrendo uno spazio angolare θ in un tempo t con moto accelerato .
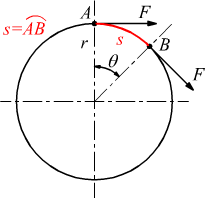
essendo s=θ·r viene eseguito un lavoro
![]() ma
M=Fr dunque
ma
M=Fr dunque
![]() [
J ]
[
J ]
Nel moto rotatorio, il lavoro espresso dal momento motore è il prodotto del momento stesso per la spazio angolare θ [rad] percorso.
Energia cinetica di rotazione
L'energia cinetica di rotazione non può essere espressa con la formula K=1/2mv2 già ottenuta per il moto di traslazione; ma se immaginiamo che un corpo rotante possa essere decomposto in tanti elementi infinitesimali di massa mi le cui velocità periferiche sono diverse tra loro, partendo dalla stessa formula, sapendo che per l'i-esimo elemento la velocità è vi=ωri con ω velocità angolare [rad/s].
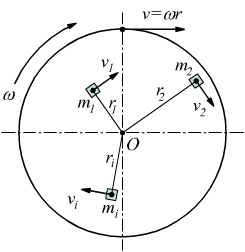

facendo la sommatoria estesa a tutti gli elementi
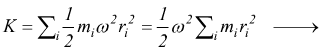
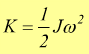
con J=momento di inerzia del corpo rispetto al proprio asse di rotazione.
La formula suddetta può anche essere ricavata dall'equazione fondamentale del moto rotatorio dove appare l'accelerazione angolare α
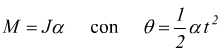
dove θ è l'angolo di rotazione eseguito nel tempo t; dalla formula del lavoro sapendo che la velocità angolare è ω=αt
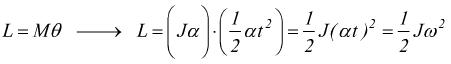
Il lavoro sviluppato dal momento motore M si converte così in energia cinetica
di rotazione 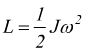
Potenza
Il lavoro è dunque una forza per uno spostamento. Per come è stato definito, il lavoro compiuto da una forza, è indipendente dal tempo impiegato per eseguire lo spostamento; eppure anche intuitivamente si comprende che a parità di forza applicata c'è una certa differenza tra far percorrere al corpo 200m in 20 secondi e percorrere la stessa distanza in un'ora. Chiaramente, la resa del lavoro è maggiore quanto minore è l'intervallo di tempo in cui viene svolto. Per misurare la rapidità con cui una forza compie un lavoro viene definita la potenza.
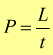 [W]
(watt=joule/sec)
[W]
(watt=joule/sec)
Bisogna notare che dal punto di vista dimensionale è
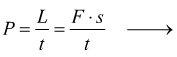
![]()
con vm=velocità media che se il moto è accelerato è data
da 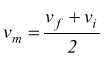
Per qualificare l'efficienza di una macchina viene, inoltre, introdotta la nozione di rendimento η.
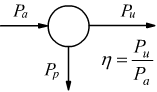
Pa=Pp+Pu=potenza assorbita
Pp=potenza persa
Pu=potenza utile
Nel caso di una coppia avremo
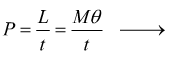
![]()
questo perchè, per definizione di velocità angolare 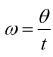
Nel moto rotatorio la potenza sviluppata da una coppia è data dal prodotto del suo momento per la velocità angolare. Nelle applicazioni pratiche dove la velocità angolare si misura in n [giri/min] dobbiamo ricordare che
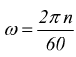 quindi
quindi
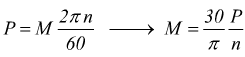
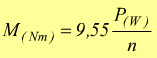 oppure
oppure 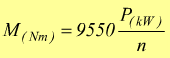
riassumendo
|
Moto traslatorio |
Moto rotatorio |
|
|
Legge del moto |
||
|
Teorema della quantità di moto |
||
|
Lavoro |
||
|
Potenza |
||
|
Energia cinetica |
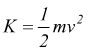 |
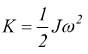 |
 edutecnica
edutecnica