Integrale doppio
Individuiamo nel piano xy un campo A di contorno (o frontiera) dove sia definita una funzione continua z=f(x,y) ad un solo valore di z. Il campo A, sia interamente contenuto in un rettangolo MNPQ, con le prerogative
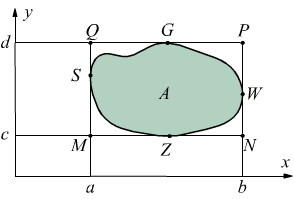
a ≤ x ≤ b
c ≤ y ≤ d
ed abbia la caratteristica che qualsiasi parallela all'asse x oppure all'asse y incontri la frontiera l al più in due punti. La frontiera è scomponibile in due coppie di curve:
La prima coppia con c ≤ y ≤ d
ZSG di equazione x=ψ1(y)
ZWG di equazione x=ψ2(y)
con c ≤ y ≤ d ; è costituita da funzioni ad un solo valore di
x
La seconda coppia con a ≤ x ≤ b
SZW di equazione y=ϕ1(x)
SGW di equazione y=ϕ2(x)
con a ≤ x ≤ b ; è costituita da funzioni ad un solo valore di
y.
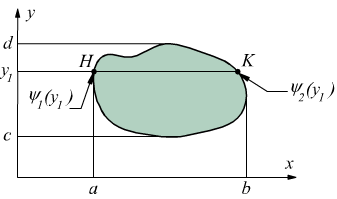
Se fissiamo un valore y=y1 con c ≤ y1 ≤
d, cioè tracciamo una retta parallela all'asse x. I punti del campo
A che hanno ordinata y1 hanno ascissa compresa tra ψ1(y1)
e ψ2(y1) (segmento HK) . In questi punti la
funzione z=f(x,y) diventa funzione della sola variabile x cioè:
z=f(x,y1) con ψ1(y1) ≤ x ≤ ψ2(y1)
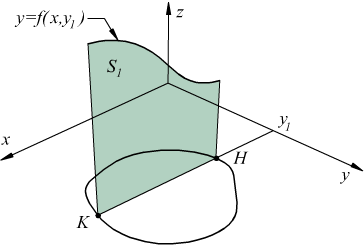
L'integrale definito ordinario
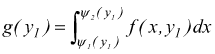
dà il valore dell'area S1 della superficie sopra il segmento
HK e sotto la linea z=f(xy).
Supponiamo che la funzione z=f(x,y) sia integrabile qualunque sia il
valore dato ad y compreso tra c e d; l'integrale:
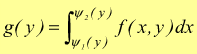 [
I ]
[
I ]
dà una funzione di y che acquista un determinato valore per ogni y in c,d. L'espressione [ I ] è dunque un integrale definito ma dipendente dal parametro y.
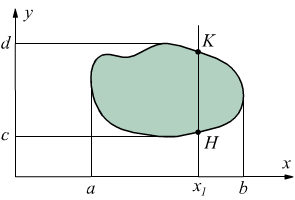
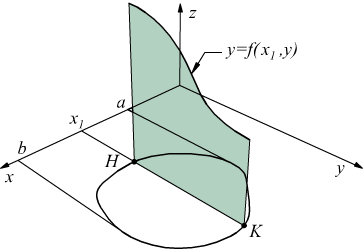
Considerando sempre il campo A e tracciando una retta parallela all'asse
y di equazione x=x1, con considerazioni analoghe a quelle
che hanno portato alla
[ I ] si giunge all'integrale definito dipendente da x che fornisce
un valore determinato, qualunque sia il valore dato ad x nell'intervallo
(a,b), valore che geometricamente rappresenta l'area della superficie
che sta sopra il segmento HK e sotto la curva z=f(x,y)
a) nel caso della [ I ] si dice che l'integrazione è fatta lungo le
linee parallele all'asse x
b) nel caso della [ II ] si dice che l'integrazione è fatta lungo le
linee parallele all'asse y
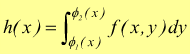 [
II ]
[
II ]
Calcolo di integrali doppi con integrazioni successive
Nell'ipotesi che la funzione g(y) della [ I ] sia continua nell'intervallo (c,d) allora esiste l'integrale definito
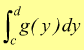 [
III ]
[
III ]
se sostituiamo la [I] nella [III]
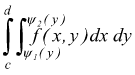
si arriva ad una espressione dall'aspetto insolito ma facile da interpretare: si calcola prima l'integrale (dipendente da y) più interno quindi quello esterno. Quest'ultima asserzione autorizza a scrivere la [ III ] come
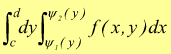 [ IV ]
[ IV ]
Sotto questa forma si intende che: prima si calcola l'integrale di
destra (che costituisce la funzione integranda dell'integrale di sinistra)
quindi si calcola l'integrale di sinistra. E' ovvio che nella prima
integrazione si considera y costante. L'espressione
[ IV ] geometricamente, descrive il volume del solido delimitato delimitato
dal campo A e dalla superficie z=f(x,y) questo tipo di solido viene
denominato cilindroide. A scopo di verifica, riprendiamo l'area S1
della superficie sopra il segmento HK data dall'integrale definito
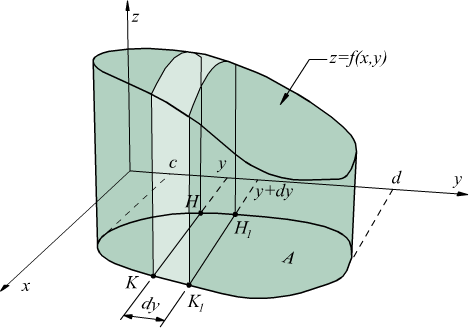
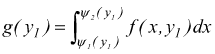
incrementando y1 di dy, il prodotto S1·dy fornisce il volume del solido sopra il settore HKK1H1 pertanto il volume del settore generico è
![]()
integrando quest'ultima tra c e d si ottiene il volume V:
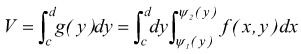 [
V ]
[
V ]
a quest'ultima, si giunge integrando per linee parallele all'asse x (HK è parallela ad x). Se si integra lungo linee parallele all'asse y si giunge al volume del cilindroide disegnato
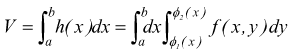 [
VI ]
[
VI ]
I due integrali [V] e [VI] possono essere formalmente scritti
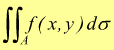 [
VII ]
[
VII ]
In quest'ultima dσ è l'elemento di superficie scelto nel campo A .Per dσ=dx·dy (area del rettangolo infinitesimo del campo A di dimensioni dx e dy) si ha
![]()
si tratta dell'integrale doppio esteso al campo A, di f(x,y) in dxdy e viene denominato integrale di campo.
Per il calcolo dell'integrale di campo si fa uso della [V] o della [VI], cioè ad integrazioni successive , a seconda che si disponga della coppia x=ψ1(y) ed x=ψ2(y) di funzioni nelle quali si spezza il campo A (integrazione per linee parallele all'asse x) oppure che si disponga della coppia y=ϕ1(x) e d y=ϕ2;(x) (integrazione per linee parallele all'asse y).
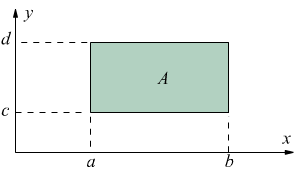
Si può notare che se il campo si riduce ad un rettangolo, la [V] e la [VI] diventano rispettivamente
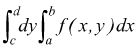 [
VIII ]
[
VIII ]
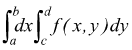 [
IX ]
[
IX ]
Esempio 1
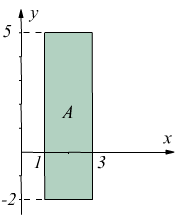
Nel disegno il campo A è definito dalle linee x=1, x=3, y=-2, y=5 .Si può integrare prima per linee parallele ad x
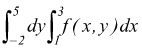
oppure si può integrare prima rispetto ad y : 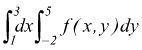
Esempio 2
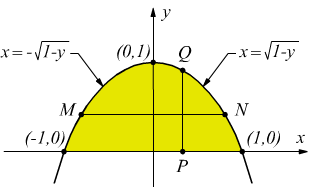
Il campo A viene
definito dalle linee y=0 ed y=1-x2.
Integrando prima rispetto ad y (per linee parallele all'asse y :segmento
PQ)
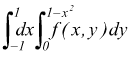
Se invece si volesse integrare prima rispetto ad x (cioè per linee
parallele all'asse x:segmento MN) si deve osservare che al variare di
y tra 0 ed 1, x varia tra l'ascissa di M e quella di N, quindi tra ![]() e
e
![]() (ottenute
dall'eq. della parabola)
(ottenute
dall'eq. della parabola)
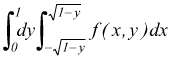
Esempio 3
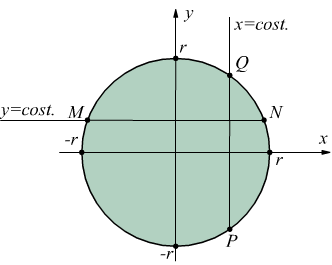
Il campo di integrazione
A è il cerchio x2+y2=r2
Per x=cost. si ha ![]() (segmento
PQ) Se integriamo prima rispetto ad y:
(segmento
PQ) Se integriamo prima rispetto ad y:
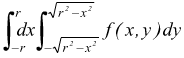
In modo analogo per x=cost. (tratto MN) si ha ![]()
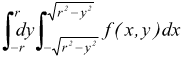
Esempio 4
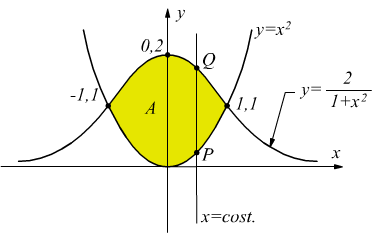
Il campo di integrazione A è definito dalle curve
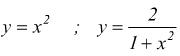
dopo aver studiato per sommi capi le due funzioni si ottiene il grafico riportato. Integrando prima rispetto ad y (segmento PQ) si ha
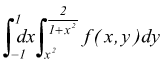
se si volesse invertire l'ordine di integrazione (cioè integrare prima
rispetto ad x) bisogna dividere il campo A tramite la retta y=1, ottenendo
i due campi A1 ed A2.
Per il campo A1 : ![]() .
Per il campo A2 essendo
.
Per il campo A2 essendo
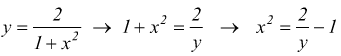 i
limiti per la x sono
i
limiti per la x sono 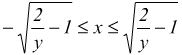
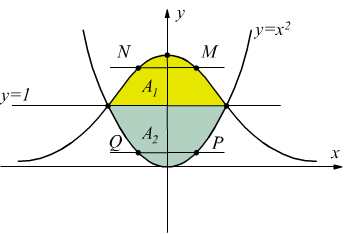
Essendo A=A1+A2
si ha 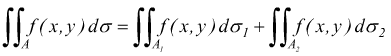 integrando
prima rispetto ad x risulta:
integrando
prima rispetto ad x risulta:
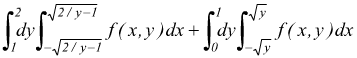
Esempio 5
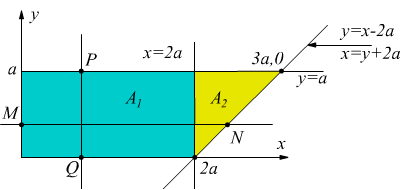
Il campo di integrazione A è definito da y=9, y=a, y=x-2a, x=0.Integrando prima, rispetto ad x (segmento MN)
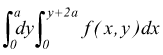
per integrare prima rispetto all'asse y (PQ:linee parallele all'asse y) occorre dividere il campo A tramite la retta x=2a
Per il campo A1: 0 ≤ x ≤2a e 0 ≤ y ≤a
Per il campo A2: 2a ≤ x ≤3a e x-2a ≤ y ≤a
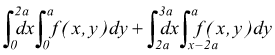
Esempio 6:calcolare l'integrale doppio 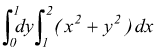
Qui viene già assegnata si la funzione integrando che l'ordine di integrazione, si applica quindi la [I ] oppure la [ II ] ricordando che mentre si esegue la prima integrazione si considera costante la variabile integrata per seconda (y qui nel nostro caso)
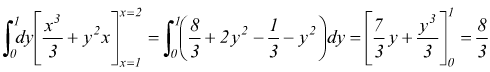
Esempio 7: calcolare
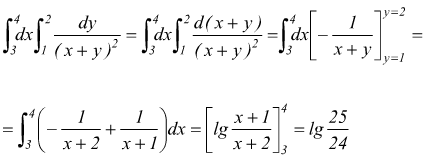
Esempio 8: calcolare
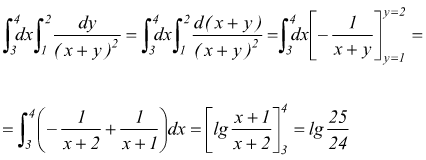
Esempio 8: calcolare
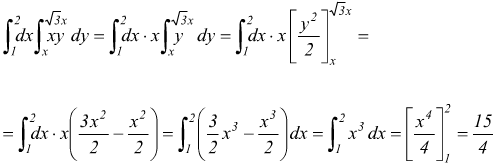
Esempio 9:calcolare
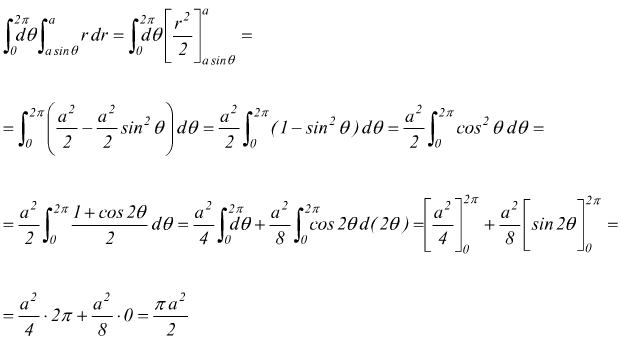
Volume di un cilindroide
Si è detto che l'integrale [ VII ] può essere usato per calcolare il volume del cilindroide delimitato dal campo A e dalla superficie z=f(x,y) bisogna comunque specificare alcune cose:
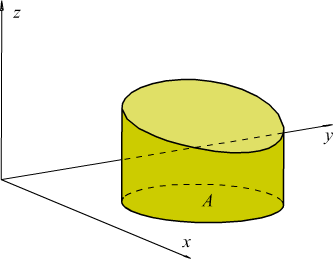
1) Il cilindroide può giacere tutto dalla parte z > 0 , quidi, tutto al di sopra del piano xy; in tal caso essendo z > 0 è sempre:
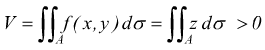
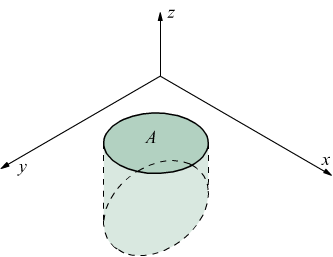
2) Il cilindroide può giacere tutto sul lato z < 0 cioè tutto sotto il piano xy; in tal caso essendo z<0 è sempre
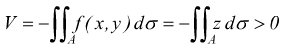

3) Il cilindroide può giacere in parte sopra ed in parte sotto il piano xy . In questo caso si cerca di suddividere A in campi la cui unione dà A ed in ognuno dei quali z acquista lo stesso segno. Ad es. in figura in A1 è sempre z >0 ed in A2 e z ≤. Il volume del cilindroide viene allora dato dall'integrale di campo
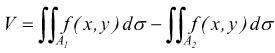
entrambi gli addendi al secondo membro sono positivi.
Coordinate polari
Un sistema di coordinate che ricorre spesso è il sistema di coordinate polari. Con questo sistema si usano le due coordinate
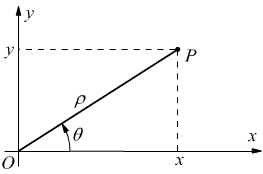
ρ:modulo
θ:argomento
Come si vede dal disegno, qualsiasi punto del piano può essere individuato indifferentemente o dalla coppia di coordinate x,y oppure dalla coppia ρ,θ. I campi di variabilità di queste ultime sono
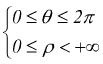
x: y: ρ: θ:
per convenzione gli angoli θ sono positivi in senso antiorario. Le formule di trasformazione tra i due sistemi di coordinate sono
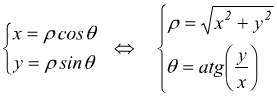
E' possibile dimostrare che per passare da coordinate cartesiane a coordinate polari si deve applicare la relazione
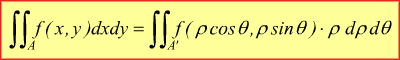
con A' il corrispondente valore dell'area A nel piano ρ-θ la precedente espressione, fornisce come si sa il volume del cilindroide delimitato da A e dalla superficie z=f(x,y). Nel caso si voglia ottenere la superficie S del campo A, basterà dunque, applicare la
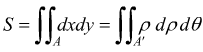
Esempio : calcolare in coordinate polari il seguente integrale
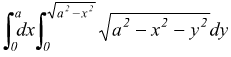
In questo caso il campo di integrazione è il cerchio di raggio a e centro nell'origine, limitato al I° quadrante.
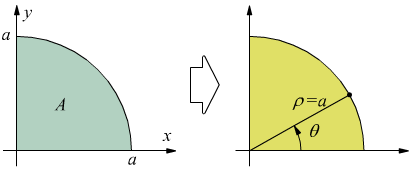
L'area A delle coordinate xy viene in questo modo espressa come 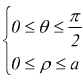
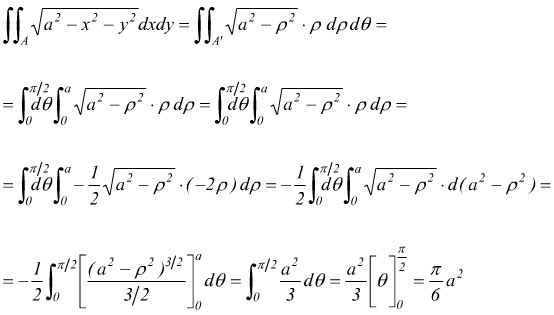
 edutecnica
edutecnica