Sistemi lineari
Un sistema lineare di n equazioni ed m incognite è rappresentato nella forma seguente
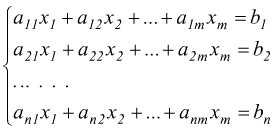
con i coefficienti delle incognite
![]()
e i termini noti
![]() assegnati
assegnati
Se tutti i termini noti sono nulli il sistema è detto lineare omogeneo.
Una soluzione del sistema assegnato è un insieme di numeri reali (m-pla) $(x↖{-}_1,x↖{-}_2,..., x↖{-}_m)$ che sostituiti alle m incognite soddisfano le n equazioni del sistema.
Risolvere un sistema significa determinare tutte le soluzioni.
Un sistema lineare con una soluzione è chiamato determinato.
Un sistema lineare con infinite soluzioni viene definito indeterminato.
Un sistema lineare con nessuna soluzione viene definito impossibile.
Questo sistema può essere espresso in forma matriciale tramite la matrice n×m dei coefficienti
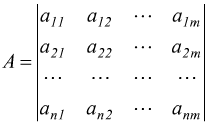
e il vettore colonna m×1 delle incognite 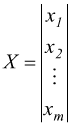
assieme al vettore colonna n×1 dei termini noti 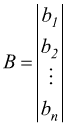
Si dimostra che vale la relazione
![]() cioè
cioè
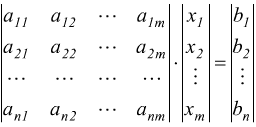
Nel caso più frequente si ha a che fare con sistemi di n equazioni in n incognite, quindi con una matrice A dei coefficienti quadrata di ordine n mentre già sappiamo come calcolare l'inverso di una matrice quadrata:
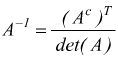
Da questa si desume che le matrici quadrate invertibili sono tutte e solo quelle con determinante diverso da zero.
ottenendo la soluzione del sistema: 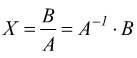
Si deduce che se la matrice A dei coefficienti è invertibile (cioè ha il determinante diverso da zero) il sistema ammette soluzione.
Teorema di Cramer
Si applica a sistemi di n equazioni in n incognite e una realizzazione informatica di questo teorema era già stata tentata in precedenza .
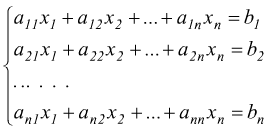
se il determinante della matrice quadrata di ordine n dei coefficienti det(A)=Δ≠0 (diverso da zero) allora, il sistema è determinato e l'unica soluzione si ottiene dividendo per Δ ciascuno degli n determinanti ottenuti da Δ sostituendo rispettivamente alla prima, seconda n-esima colonna il vettore-colonna dei termini noti.
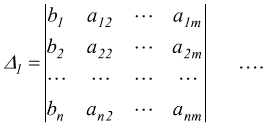
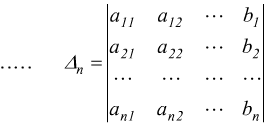
La soluzione del sistema assegnato vale
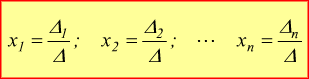
Teorema di Rouché-Capelli
Consideriamo questi due sistemi
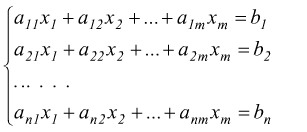
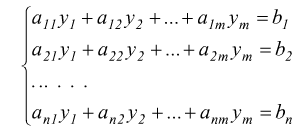
possiamo dire che rappresentano lo stesso sistema, dato che un sistema non dipende da come chiamiamo le incognite ma solo dai coefficienti di queste e dai termini noti. Questi dati caratteristici possono essere descritti da queste due matrici
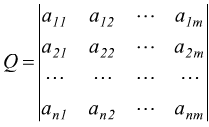 matrice
incompleta del sistema
matrice
incompleta del sistema
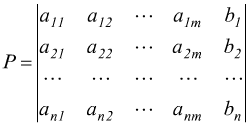 matrice
completa del sistema
matrice
completa del sistema
Condizione necessaria e sufficiente affinché un sistema lineare di n equazioni in m incognite sia possibile è che la matrice incompleta e quella completa abbiano lo stesso rango.
Ipotizziamo che il sistema sia possibile e che vi sia un rango comune
q≤n
q≤m
Scegliamo fra le n equazioni che compongono il sistema q equazioni e
teniamo in ciascuna equazione al primo membro le q incognite i cui coefficienti
hanno contribuito alla formazione del minore non nullo , mentre le altre
(m-q) incognite si trasportano al secondo membro considerandole come quantità
note (parametri) si ottiene così un sistema di q equazioni in q incognite
con determinante diverso da zero. Si applica ad esso la regola di Cramer.
Risolto il sistema si ottengono le q incognite in funzione delle (m-q)
incognite che erano state considerate, durante la risoluzione del sistema
quantità note. Poiché a ciascuna delle (m-p) incognite possiamo attribuire
infiniti valori si dice che il sistema ammette ∞ m-p
soluzioni; il numero m-p restituisce il grado di indeterminazione del
sistema.
Indicando con
Δ:determinante della matrice incompleta
q:rango della matrice incompleta
p:rango della matrice completa.
In base al teorema di Capelli si possono stabilire i seguenti casi.
Sistema lineare di n equazioni in n incognite
Se Δ ≠0 il sistema è determinato e
la soluzione si trova con la regola di Cramer
Se Δ=0 si applica il teorema di Capelli e si possono presentare
due casi
q=p il sistema è indeterminato e ha n-p soluzioni
q≠p il sistema è impossibile.
Sistema lineare di n equazioni in m incognite
q≠p il sistema è impossibile
q=p il sistema è possibile e si possono presentare due casi
se q=m il sistema ha una sola soluzione
se q < m il sistema ha ∞ m-p soluzioni.
Sistema omogeneo di n equazioni in n incognite
Se Δ ≠0 il sistema ammette solo la
soluzione nulla xi=0 (i=1,2,..,n)
Se Δ=0 il sistema ha infinite soluzioni compresa quella nulla.
Sistema omogeneo di n equazioni in m incognite
Se q=m il sistema ammette solo la soluzione
nulla xi=0 (i=1,2,..,n)
Se q < m il sistema ha ∞ m-p soluzioni compresa la soluzione
nulla.
 edutecnica
edutecnica