Matrici
La tabella di n×m numeri, ( con n,m>1) come la seguente
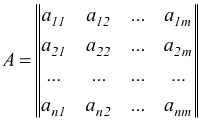
viene chiamata matrice di n righe e di m colonne o matrice n×m.
Ogni elemento è individuato da una coppia di pedici: il primo indica la
riga il secondo la colonna.
Così con a21 si indica l'elemento che occupa la seconda riga
e la prima colonna.
Una generica matrice può essere indicata come
![]() con
j=1,2,..n e k=1,2,..m
con
j=1,2,..n e k=1,2,..m
Due matrici ![]() e
e ![]() con
j=1,2,..n e k=1,2,..m sono uguali se
con
j=1,2,..n e k=1,2,..m sono uguali se ![]()
Se n=m la matrice si dice quadrata di ordine
n.
Se n≠m si dice rettangolare.
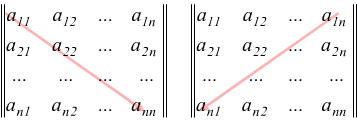
In una matrice quadrata di ordine n gli elementi coi pedici uguali :a11,
a22…,ann formano la diagonale
principale. Gli elementi a1n,a2(n-1),.. an1
costituiscono la diagonale
secondaria.
Le matrici più importanti sono:
matrice nulla
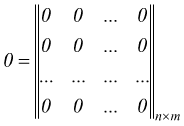 La
matrice può essere di qualsiasi ordine
La
matrice può essere di qualsiasi ordine
matrice unitaria
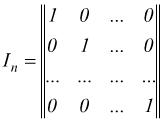
è una matrice quadrata di ordine n con tutti gli elementi della diagonale principale uguali a 1 e tutti gli altri elementi nulli.
Matrice diagonale:
è una matrice quadrata di ordine n
con tutti gli elementi nulli tranne quelli della diagonale principale.
Matrice 1×m
![]()
è una matrice con una sola riga, viene anche chiamata vettore-riga.
Matrice n×1
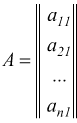
è una matrice con una sola colonna, viene anche chiamata vettore colonna.
Matrice trasposta
Se abbiamo una matrice A e in essa si scambiano ordinatamente le righe
con le colonne si ottiene una nuova matrice detta trasposta
di A e si indica AT.
![]() con
con
![]() con
j=1,2,..n e k=1,2,..m
con
j=1,2,..n e k=1,2,..m
Se A è una matrice n×m, la trasposta AT è una matrice m×n.
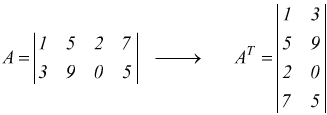
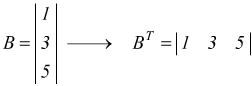
Matrice simmetrica
Una matrice quadrata A è simmetrica se coincide con la sua trasposta cioè
se ogni riga coincide con la colonna di ugual pedice.
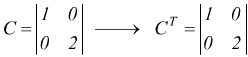
Operazioni sulle matrici
E' possibile stabilire un'algebra per insieme delle matrici, come nel caso degli insiemi numerici,
Se ![]() e
e
![]() sono due matrici n×m la somma di A e B:
sono due matrici n×m la somma di A e B:
![]() con
j=1,2,..n e k=1,2,..m
con
j=1,2,..n e k=1,2,..m
L'addizione delle matrici A e B è possibile solo se hanno lo stesso numero di righe e lo stesso numero di colonne.
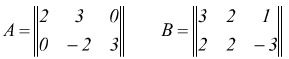
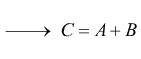
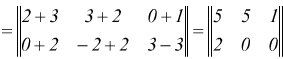
L'addizione fra matrici gode delle proprietà commutativa ![]()
e della proprietà associativa ![]()
Prodotto di una matrice per uno scalare
Se ![]() è
una matrice n×m e h è un numero reale, per prodotto di h per A si
intende la matrice n×m data da:
è
una matrice n×m e h è un numero reale, per prodotto di h per A si
intende la matrice n×m data da: ![]() .
Ad esempio
.
Ad esempio
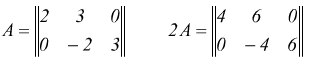
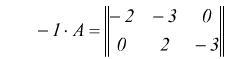
per l''insieme delle matrici valgono le seguenti identità
1 Proprietà distributiva della moltiplicazione rispetto all'addizione fra numeri reali
![]()
2 Proprietà distributiva della moltiplicazione rispetto all'addizione fra matrici n×m
![]()
3 ![]()
4 ![]()
5 ![]()
Prodotto di matrici
Se ![]() è
una matrice n×r e
è
una matrice n×r e ![]() è
una matrice r×m si definisce il prodotto delle matrici A e B la
matrice n×m
è
una matrice r×m si definisce il prodotto delle matrici A e B la
matrice n×m
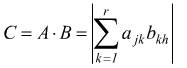
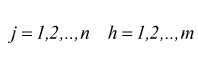
In base alla definizione:
A ] La moltiplicazione di due matrici A e B è possibile solo se il
numero delle colonne di A è eguale al numero delle righe di B.
B ] La matrice, il prodotto di due matrici A e B, ha tante righe
quante sono quelle di A e tante colonne quante sono quelle di B
C ] Posto ![]() l'elemento
cjh è è il prodotto scalare della j-esima riga di A per la
h-esima colonna di B, dunque, il prodotto di due matrici si calcola righe
per colonne .
l'elemento
cjh è è il prodotto scalare della j-esima riga di A per la
h-esima colonna di B, dunque, il prodotto di due matrici si calcola righe
per colonne .

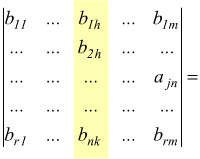
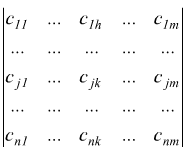
![]()
Esempio: calcolare il prodotto delle due matrici
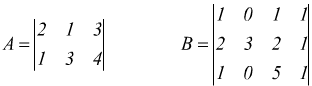
La moltiplicazione è possibile in quanto la prima matrice è 2×3 e la seconda una 3×4, per cui il numero delle colonne di A è uguale a quello delle righe di B.
Posto ![]() si
avrebbe
si
avrebbe
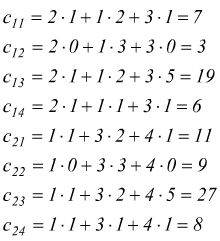
Risulta 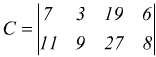
Sempre in base alla definizione, si intuisce come se A è moltiplicabile per B non è detto che B sia moltiplicabile per A; cioè B·A potrebbe essere priva di significato, questo accade se il numero di colonne di B non è uguale al numero di righe di A . Nel caso di matrici quadrate esistono sia i prodotti AB che BA ma in generale non vale la proprietà commutativa; cioè
![]()
Matrici quadrate
Se consideriamo solo l'insieme delle matrici quadrate, notiamo come le operazioni di addizione e sottrazione hanno le stesse caratteristiche delle stesse operazioni fra dei numeri reali, mentre per il prodotto c'è qualche limitazione come abbiamo visto, anche se rimangono valide la proprietà associativa e la proprietà distributiva rispetto all'addizione. Bisogna inoltre ricordare le matrici divisori dello zero. Notiamo come
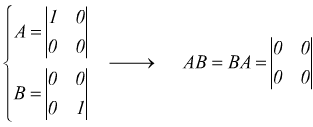
cioè pur non essendo nulle (ne A ne B) il loro prodotto è una matrice nulla; questa caratteristica è nota come legge dell'annullamento del prodotto, e le matrici A e B si dicono divisori dello zero.
Determinante
Ad ogni matrice quadrata A è possibile associare un numero reale chiamato determinante della matrice, normalmente indicato det(A). Per il suo calcolo bisogna solitamente passare attraverso la definizione di minore complementare dell'elemento ajk della matrice A di ordine n che è il determinante della matrice di ordine (n-1) ottenuta da A sopprimendo la j-esima riga e la k-esima colonna. Se indichiamo con Mjk il minore complementare di ajk si può definire il complemento algebrico ( o cofattore ) di ajk il numero Ajk:
![]()
cioè Ajk coincide con Mjk oppure col suo opposto a secondo che la somma j+k sia pari o dispari.
Si definisce determinante di una matrice quadrata A di ordine n>1 il numero reale
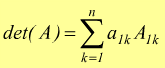
cioè, la sommatoria degli n elementi della prima riga moltiplicati per i rispettivi complementi algebrici.
se, invece, n=1 si ha A=|a|=det(A).
Determinante di ordine 2
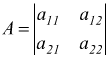 con
con 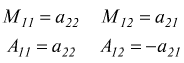
![]()
cioè il determinante di una matrice quadrata di ordine n=2 si ottiene sottraendo al prodotto degli elementi della diagonale principale il prodotto degli elementi della diagonale secondaria.
Determinante di ordine 3
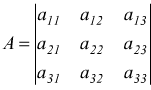 si
ha
si
ha ![]()
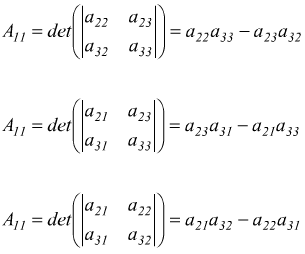
in definitiva
![]()
![]()
La regola di Sarrus
E' una comoda regola mnemonica che permette di ricordarsi schematicamente
la formula risolutiva del determinante di una matrice di ordine 3 ( e
solo di ordine 3 ) consiste nell'accostare
a destra della matrice le prime due colonne della matrice stessa.
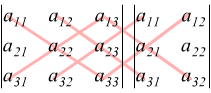
Il determinante è uguale alla somma dei prodotti degli elementi della diagonale principale e delle sue due parallele a cui si sottrae la somma dei prodotti della diagonale secondaria e delle sue parallele.
Proprietà dei determinanti
1 Il calcolo di un determinante può essere eseguito
rispetto ad una linea ( riga o colonna ) qualsiasi.
secondo una riga i scelta arbitrariamente 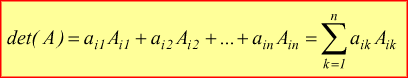
secondo una colonna j scelta arbitrariamente 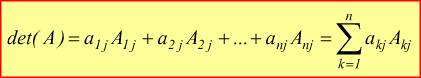
2 Cambiando ordinatamente le righe con le
colonne e le colonne con le righe il determinante non cambia.
3 Se gli elementi di una linea (riga o colonna)
sono nulli, il determinante è nullo.
4 Se si cambiano di posizione due linee parallele
il determinante cambia di segno.
5 Se due linee parallele sono proporzionali
(o uguali) il determinante è nullo.
6 La somma algebrica dei prodotti degli
elementi di una linea per i complementi algebrici di una linea parallela
è uguale a zero.
7 Se si moltiplicano gli elemnti di una
linea per k, il determinante viene moltiplicato per k.
8 Se gli elementi di una linea sono polinomi
di h termini, il determinante è uguale alla somma di h determinanti che
si ottengono sostituendo nel determinante dato a ciascun polinomio il suo
primo, secondo,..h-esimo termine che è come dire
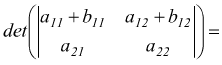
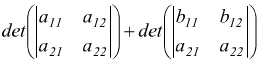
9 Il valore di un determinante non cambia se ad una linea viene addizionata una combinazione lineare di una o più linee parallele.
Matrice inversa
Nel caso dei numeri reali la nozione di inverso di un numero è molto semplice; se n≠0 allora 1/n è il suo inverso. Formalmente una matrice inversa può essere definita nel modo seguente.
Una matrice quadrata A di ordine n è invertibile se esiste una matrice A-1 per la quale
![]()
Se la matrice A-1 esiste viene chiamata matrice inversa di A.
Per l'elemento neutro In non ci sono problemi; si verifica facilmente
![]() ogni
matrice In ammette come inversa se stessa.
ogni
matrice In ammette come inversa se stessa.
Ogni matrice diagonale è invertibile; è facile verificare che
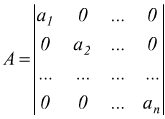 ammette
come inversa
ammette
come inversa 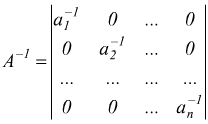
ad esempio se
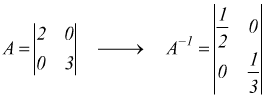
La matrice cofattore Ac associata ad una matrice quadrata A si ottiene sostituendo ogni elemento di quest'ultima col suo cofattore ( complemento algebrico ). Se det(A)≠0 allora
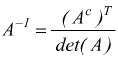
Matrici e vettori
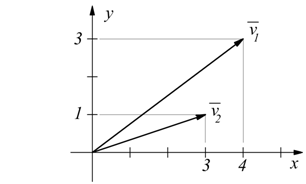
Sul piano cartesiano consideriamo i due vettori, con
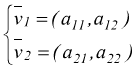
a11 e a12= componenti cartesiane del primo
vettore
a21 e a22= componenti cartesiane del secondo
vettore
se le loro componenti sono proporzionali i due vettori sono sicuramente paralleli ( e collineari)
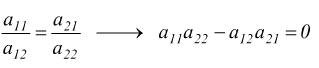
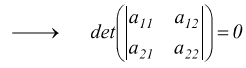
quindi due vettori sono paralleli se il determinante della matrice composta dalle loro componenti è nullo.
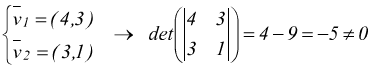
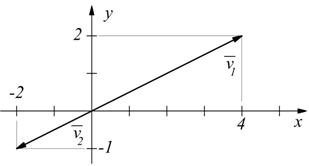
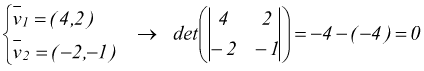
Matrici ed equazione della retta
Ipotizziamo una retta r definita dal passaggio passante fra i due punti S(x1,y1) e T(x2,y2) il vettore v rappresentativo il segmento ST ha come componenti
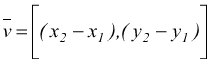
il vettore p rappresentativo il segmento SP ha come componenti 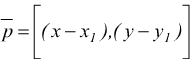
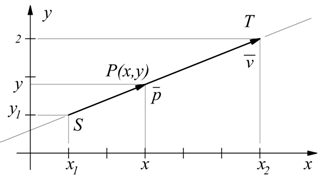
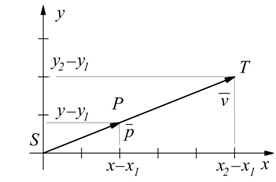
dopo aver effettuato una opportuna trasformazione per far coincidere il punto di applicazione dei due vettori con l'origine degli assi, si vede come questi due vettori debbano essere paralleli affinché il punto P debba appartenere alla retta r.
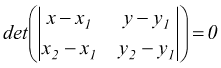 infatti
infatti
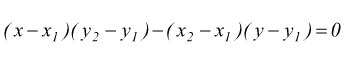
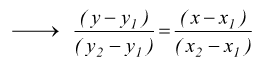
Rango di una matrice
Consideriamo la generica matrice di n righe ed m colonne per ipotesi con n≤m
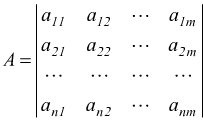
Da questa matrice possiamo scegliere arbitrariamente k righe e k colonne con k≤n≤m ottenendo una sottomatrice quadrata di ordine k il cui determinante si chiama minore di ordine k .
La caratteristica o rango di una matrice A
n×m, è l'ordine massimo dei suoi minori non tutti nulli.
Il calcolo del rango di una matrice è semplificato dal teorema di Kronecker:
Affinché una matrice abbia caratteristica q è che vi sia in essa una matrice Aq di ordine q che ha determinante non nullo e che ogni altra sottomatrice di ordine q+1 che contenga Aq abbia determinante nullo.
Ad es.
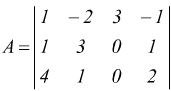
La matrice è 3×4 quindi il rango può essere al massimo Rk=3; q≥1
in quanto non tutti gli elementi della matrice sono nulli.
Una sottomatrice di ordine 2 con determinante non nullo estratta dalla
matrice A sarebbe:
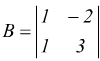 quindi
q≥2
quindi
q≥2
Le possibili sottomatrici che contengono B sono:
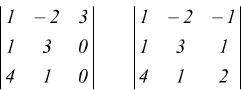 ambedue
con determinante non nullo; quindi Rk(A)=q=3
ambedue
con determinante non nullo; quindi Rk(A)=q=3
Ad.es.
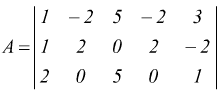
La matrice è 3×5 quindi il rango può essere al massimo Rk=3 q≥1
in quanto non tutti gli elementi della matrice sono nulli.
Una sottomatrice di ordine 2 con determinante non nullo estratta dalla
matrice A
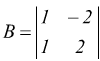 quindi
q≥2 .
quindi
q≥2 .
Le possibili sottomatrici che contengono B sono
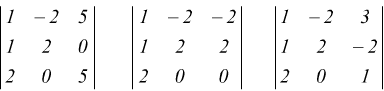 tutte
con determinante nullo
tutte
con determinante nullo
pertanto Rk(A)=q=2.
Ad.es.
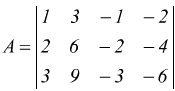
La matrice è 3×4 quindi il rango può essere al massimo Rk=3 q≥1 in quanto non tutti gli elementi della matrice sono nulli.
Notiamo come ciascuna riga sia una combinazione lineare delle altre due; qualsiasi sottomatrice 3×3 o 2×2 deve necessariamente avere determinante nullo in conseguenza della proprietà V) del determinante: se due linee parallele sono proporzionali (o uguali) il determinante è nullo consegue che
Rk(A)=q=1.
Oltre al metodo dei minori, può essere applicato in alternativa il metodo ad eleminazione gaussiana come riportato sotto:
 edutecnica
edutecnica