Distribuzione normale

     

La distribuzione normale, anche conosciuta come distribuzione gaussiana, è una delle distribuzioni di probabilità più importanti e ampiamente utilizzate in statistica; è caratterizzata da una forma a campana simmetrica e viene descritta da due parametri: la media e la deviazione standard.

Nella distribuzione normale, la maggior parte dei dati si concentra intorno alla media e la distribuzione dei dati segue una forma simmetrica rispetto alla media; inoltre, il 68% dei dati si trova entro una deviazione standard dalla media, il 95% entro due deviazioni standard e il 99.7% entro tre deviazioni standard.

La distribuzione normale è utile in statistica perché molte variabili reali, come altezza, peso e punteggi nei test standardizzati, seguono approssimativamente una distribuzione normale, Questo permette di utilizzare tecniche statistiche basate sulla distribuzione normale per analizzare e interpretare i dati in modo efficace.

Questa distribuzione è stata individuata nel 1733 da De Moivre come mezzo per dare una valutazione approssimata della funzione di probabilità binomiale; ha , successivamente, acquisito importanza quando nel 1809 Gauss ne fece uso nel contesto della teoria degli errori.
Si considera una grandezza X definita in tutto il campo reale ( $-∞ ; +∞$ ).

X ha una distribuzione di probabilità normale se la sua densità di probabilità risulta essere

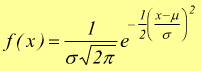
con σ = deviazione standard (scarto quadratico medio) e μ = media.
Se X ha una distribuzione normale di probabilità descritta dalla formula suddetta, X viene detta variabile normale.
Le caratteristiche fondamentali della f(x) sono:

● la forma a campana
● la simmetria rispetto al valor medio μ il che significa che le estremità sinistra e destra sono speculari.
● la media (il valore medio), la moda (il valore più frequente) e la mediana (il valore centrale) sono tutti uguali e si trovano al centro della distribuzione.
● il massimo per x= μ quando l'ordinata vale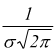
● quanto più x si allontana da μ tanto più f(x) decresce tendendo asintoticamente a zero
● i punti μ+σ e μ-σ sono punti di flesso.

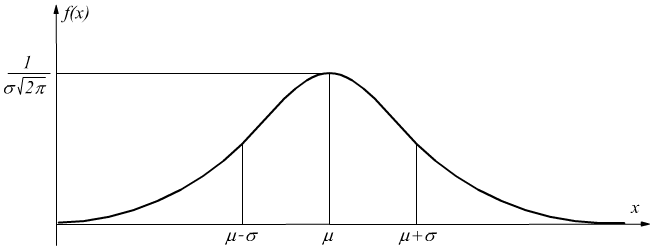
Il valore di μ viene anche indicato come centro della distribuzione e caratterizza la posizione della curva rispetto all'asse delle ordinate.
Al variare di μ la curva si sposta lungo l'asse x, ma resta invariata la sua forma.

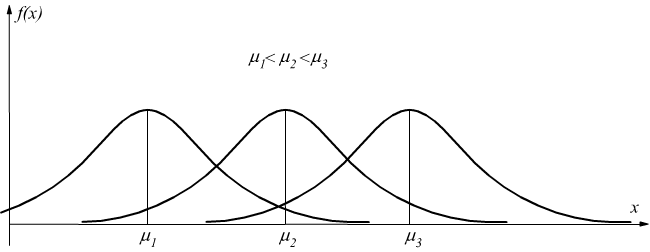
Il parametro σ, caratterizza la forma della curva, dato che rappresenta la dispersione dei valori attorno al massimo della curva.

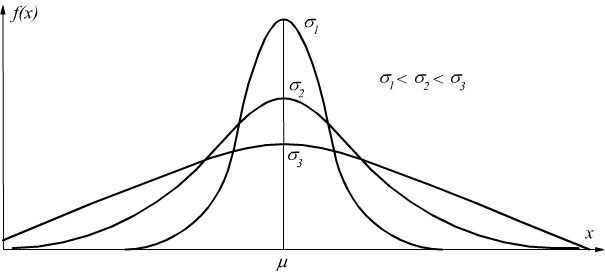
all'aumentare di σ la curva si appiattisce e si allarga, mentre al diminuire di σ la curva si restringe e si alza.

Per determinare la probabilità che la variabile aleatoria assume in un determinato intervallo (a,b) è necessario calcolare l'area sottesa alla curva compresa tra a e b.

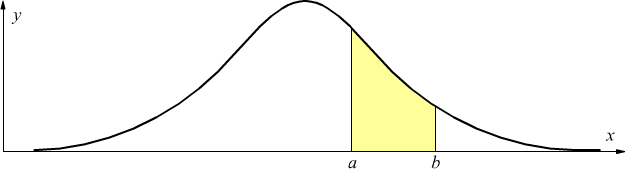
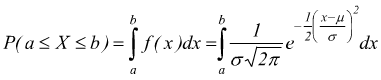
Non si tratta di un integrale semplice da risolvere perchè si devono applicare procedimenti di sviluppo in serie, che comunque portano a valori approssimati che dipendono, inoltre, da μ e da σ.

Per superare questo problema, si fa una trasformazione di variabile e si pone:

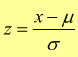      La funzione densità di probabilità di z :          

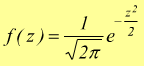
Questa viene chiamata funzione di densità di probabilità della distribuzione normale ridotta.

In base alla precedente trasformazione è possibile determinare la probabilità che una generica variabile aleatoria X con media μ e deviazione standard σ appartenga ad un intervallo (a,b).

esistono infinite curve che approssimano a tale funzione al variare di μ e σ.
La curva a cui ci si può sempre ricondurre (con un'opportuna trasformazione) è la curva della distribuzione normale standardizzata. con parametri :
media: μ= 0
deviazione standard: σ= 1

z è la variabile normale standardizzata. La curva che la rappresenta volge la sua concavità verso il basso nell'intervallo (-1, 1) i punti di ascissa z=±1 sono dei flessi.

Il 68,26% dei valori è compreso fra -1 e +1.
Il 95,44% dei valori è compreso fra -2 e +2.
Il 99,73% dei valori è compreso fra -3 e +3.

Un'area di probabilità del 95% è compresa fra ±1,96
Un'area di probabilità del 99% è compresa fra ±2,576

Attraverso la trasformazione lineare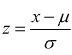       

è possibile determinare la probabilità che una generica variabile aleatoria X, con media μ e deviazione standard σ appartenga ad un intervallo (a,b). Valori indicativi della funzione di probabilità sono riportati nella tabella allegata.
Se vogliamo calcolare P(X≤x_o) notiamo che

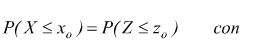
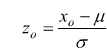
in modo analogo per calcolare P(x₁≤X≤x₂)

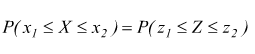
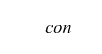
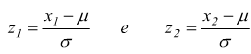
Facciamo un esempio, supponiamo di misurare il peso di 1000 individui rilevando un valore medio μ=70kg con uno scarto quadratico medio σ=8kg; vogliamo determinare la probabilità che:
A i pesi siano compresi tra 60kg e 70kg
B i pesi siano esterni all'intervallo tra 65kg e 75kg
C i pesi siano superiori a 80kg
D i pesi siano inferiori a 60kg.

punto A per x₁=60 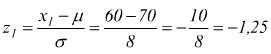       dalle tabelle della distribuzione normale
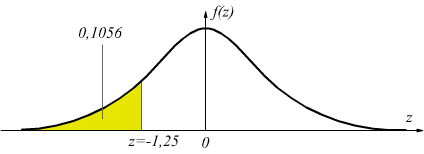
leggiamo una probabilità cumulativa per valori negativi di z con z₁=-1,25 corrispondente ad una probabilità p(z₁≤-1,25)=0,1056

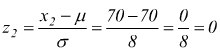     ovviamente p(z₂≤0)=0,5. Sottraendo le due aree p(-1,25≤z≤0)=0,5-0,1056=0,3944

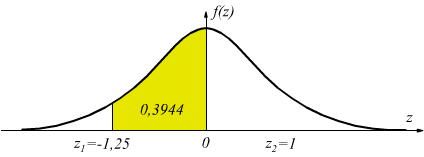
ci saranno 1000·0,3944=394,4 (almeno 394) soggetti di peso compreso tra 60 e 70kg.

Punto B per i pesi esterni all'intervallo tra 65kg e 75kg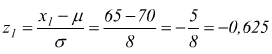       

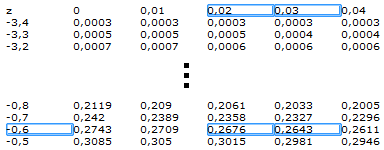
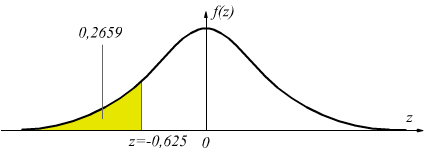
dalle tabelle della probabilità cumulativa per valori negativi di z con z₁=-0,625 si trova una probabilità che possiamo ritenere
p(z₁≤-0,625)=0, 2659

mentre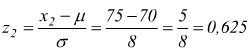    

dalle tabelle della probabilità cumulativa per valori positivi di z con z₂=0,625 si trova una probabilità che possiamo ritenere
p(z₂≤ 0,625)= 0,734, ovviamente a noi interessa la probabilità p(z₂≥ 0,625)= 1-0,734,= 0,2659 identico al precedente come era prevedibile.

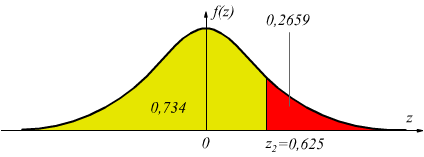
La probabilità complessiva di trovare un soggetto che abbia un peso inferiore a 65kg oppure maggiore di 75kg è 2·02659= 0,5318

Punto C per trovare la probabilità di trovare un soggetto che pesa di più di 80kg è facile

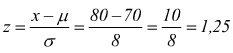
dalle tabelle della probabilità cumulativa per valori positivi di z=1,25 si trova una probabilità che possiamo ritenere p(z≤ 1,25)= 0,8944, ovviamente a noi interessa la probabilità p(z≥ 1,25)= 1-0,8944=0,1056 come dire che su 1000 soggetti 1000·0,1056=105,6 (105 diremo) hanno la probabilità di pesare più di 80kg.

Punto D trovare chi pesa meno di 60kg. è ancora più facil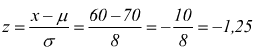e     sa come si è giò visto al punto A p(z≤-1,25)=0,1056

Come si vede, noti i parametri della variabile aleatoria X, le probabilita cercate possono essere trovate manualmente (con le tavole) oppure automaticamente, tramite il modulo seguente.