Parabola
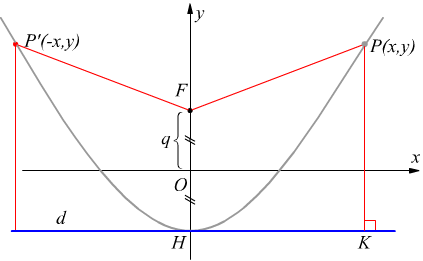
La parabola è il luogo geometrico dei punti di un piano equidistanti da un punto fisso F chiamato fuoco e da una retta assegnata d chiamata direttrice.
Disegniamo una coppia di assi cartesiani ortogonali, con l'asse y che passa per il fuoco F e che sia perpendicolare alla retta d. Facciamo in modo che l’origine degli assi O sia equidistante dalla retta direttrice d e dal fuoco F.
In questo modo l’origine degli assi O diventerà il vertice della parabola. L’asse x sarà parallelo alla direttrice d.
La retta passante per il vertice e perpendicolare alla direttrice sarà
l'asse di simmetria della parabola e in questo caso coinciderà con l'asse
y; infatti se un punto P appartiene al luogo, cioè è equidistante da d e
da F, anche il punto P’ simmetrico rispetto a P rispetto a tale asse appartiene
al luogo.
Diciamo q l’ordinata di F ed (x,y) le coordinate di un punto qualsiasi P
della parabola. Se K è il piede della perpendicolare tracciata da P sulla
retta d, sarà
![]()
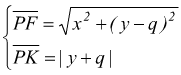 si
ha
si
ha
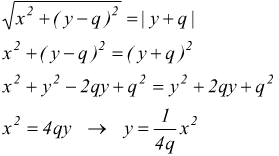
se poniamo 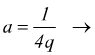
![]()
Questa è l'equazione di una parabola con il vertice nell'origine O, con l'asse di simmetria coincidente con l'asse y e con il fuoco nel punto di coordinate `F(0,1/(4a)) ` con la retta direttrice che ha equazione `y=-1/(4a) `.
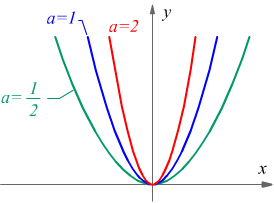
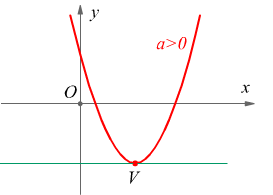
se a > 0 la parabola è contenuta nel semipiano superiore delle ordinate positive o nulle, dunque si dice che essa ha la concavità rivolta verso l'alto, in questo caso il vertice della parabola è il punto di ordinata minima O=V=(0,0) origine degli assi xy.
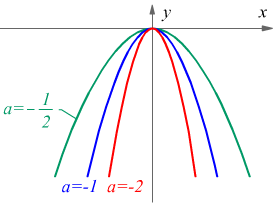
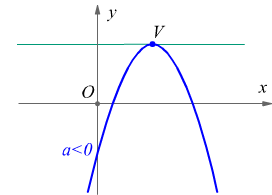
se a < 0 la parabola è contenuta nel semipiano inferiore, quello delle ordinate negative o nulle; perciò si dice che ha la concavità rivolta verso il basso; in questo caso il vertice della parabola è il punto di ordinata massima O=V=(0,0) origine degli assi xy.
L'equazione y=ax2 è anche nota come equazione canonica della parabola; la sua forma molto semplice è dovuta al fatto che il sistema di riferimento è stato scelto in modo opportuno; se fosse stato scelto un altro sistema di riferimento, l'equazione sarebbe stata diversa.
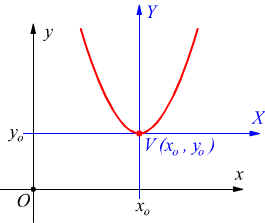
Infatti consideriamo nel sistema di riferimento xOy una generica parabola
con vertice nel punto V(xo,yo) ed asse di simmetria
parallelo all'asse y.
Eseguiamo una traslazione di assi che porti l'origine O in V. In questo
modo nel sistema XVY l'equazione della parabola sarà
![]()
le equazioni che legano tra loro i due sistemi di riferimento sono
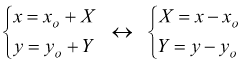
applicando queste trasformazioni alla Y=aX2 troviamo
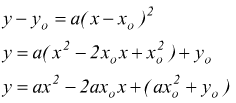 si
pone
si
pone 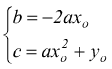
e otteniamo l'equazione completa della parabola chiamata anche funzione quadratica.
![]()
una qualsiasi parabola con asse di simmetria parallelo all'asse y è descritta da questo tipo di funzione dove al secondo membro appare un trinomio di secondo grado. Tenendo conto delle relazioni trovate
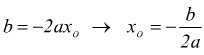 è
l'ascissa del vertice V(xo,yo) poi, sostituendo nell'equazione
completa
è
l'ascissa del vertice V(xo,yo) poi, sostituendo nell'equazione
completa
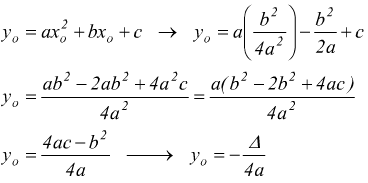
se poniamo ![]() si
ha
si
ha 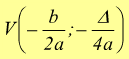 coordinate
del vertice
coordinate
del vertice
Nel sistema di riferimento XOY le coordinate del fuoco sarebbero `F(0,1/(4a)) ` per trovare le stesse coordinate nel sistema xOy
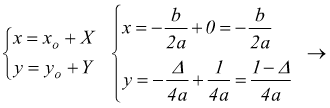
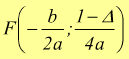 coordinate
del fuoco
coordinate
del fuoco
poi sapendo che nel sistema XOY la direttrice ha equazione si ha 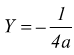 si
ha
si
ha
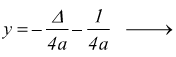
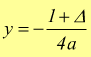 equazione
della direttrice
equazione
della direttrice
Dunque, anche il grafico della funzione y=ax2+bx+c è una parabola, tuttavia mentre la parabola di equazione y=ax2 ha vertice nell'origine e asse coincidente con l'asse y, la parabola di, la parabola y=ax2+bx+c può avere il vertice in un punto qualsiasi del piano cartesiano e ha l'asse parallelo (ma non necessariamente coincidente) all'asse y : se a > 0 la parabola è tutta contenuta nel semipiano al di sopra della retta orizzontale passante per il vertice, perciò si dice che ha ancora la concavità rivolta verso l'alto; se invece a < 0 la parabola è tutta contenuta el semipiano al di sotto della retta orizzontale passante per il vertice, perciò si dice ancora che ha la concavità rivolta verso il basso.
se a=0 non si può più parlare di una parabola perché y=bx+c vede al secondo membro un'espressione di primo grado nella variabile x e l'ntera equazione rappresenterebbe una retta.
xMin : xMax :
yMin : yMax :
Tracciare il grafico di una parabola
In base a questi pochi criteri è facilmente possibile disegnare il grafico di una qualsiasi parabola.
Ad esempio prendiamo la ![]()
Determiniamo il vertice della parabola. Notiamo che a > 0 dunque la
parabola avrà la concavità rivolta verso l'alto.
Abbiamo a=1, b=-8, c=7 troviamo le coordinate del vertice
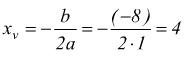 poi
poi
![]()
dunque V(4,-9). L'asse della parabola è la retta verticale passante per
V, quindi ha equazione x=4.
I punti di intersezione con l'asse x appartengono sicuramente alla parabola
quindi le loro coordinate devono soddisfare l'equazione stessa, inoltre
nei punti di intersezione con l'asse delle ascisse vale la condizione y=0
dunque risolvendo l'equazione di secondo grado ![]() si ha
si ha
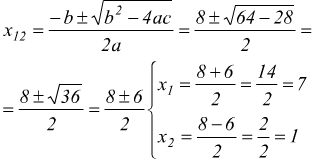
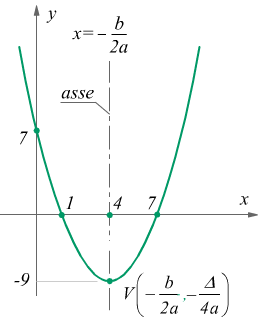
poi possiamo determinare il punto di intersezione della parabola con l'asse delle y: questo avviene quando è vera la condizione x=0.
Poi, sostituendo questo valore all'interno dell'equazione assegnata si ha
![]()
Interpretazione grafica di una equazione di secondo grado completa
In pratica per trovare l'intersezione con l'asse x bisogna eseguire un
sistema tra l'equazione della parabola in questione e l'equazione y=0 che
descrive tale asse.
Questo conduce al problema della risoluzione dell'equazione di secondo grado
ax2+bx+c=0
Tenendo presente che le soluzioni di questa equazione rappresentano le ascisse
degli eventuali punti di intersezione con l'asse x della parabola di equazione
y= ax2+bx+c possiamo dare una interpretazione grafica di una
equazione di secondo grado facendo riferimento al caso in cui sia sempre
a > 0 (parabola con la concavità rivolta verso l'alto).
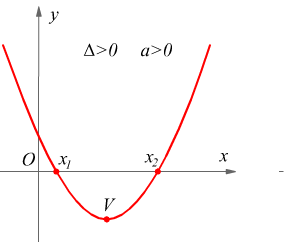
![]()
l'equazione y= ax2+bx+c ha due soluzioni reali e distinte x1 ed x2, quindi la funzione y= ax2+bx+c ha due zeri, cioè il suo grafico interseca l'asse x in due punti distinti.
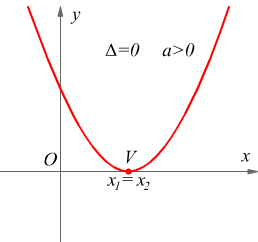
![]()
l'equazione y= ax2+bx+c ha due soluzioni reali coincidenti x1=x2, quindi la funzione y= ax2+bx+c ha due zeri coincidenti, cioè il suo grafico è tangente all'asse x.
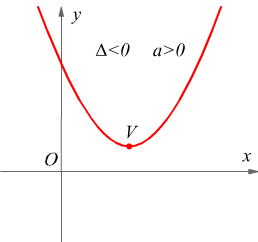
![]()
l'equazione y= ax2+bx+c non ha soluzioni reali coincidenti dunque la funzione y= ax2+bx+c non ha zeri, cioè non interseca l'asse x in alcun punto.
Interpretazione grafica di una equazione di secondo grado incompleta
Quando il trinomio di secondo grado che caratterizza l'equazione di una parabola non si presenta in forma completa si hanno da subito degli indizi sull'eventuale comportamento della curva, questo a partire dalla collocazione delle radici sul piano cartesiano che, ricordiamo, si trovano ponendo la condizione y=0 per la funzione (le intersezioni con l'asse x si trovano sempre alla quota y=0).
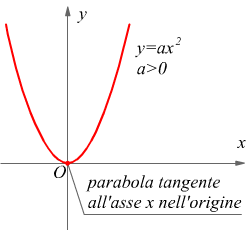
Equazione monomia
![]()
questa equazione ha due soluzioni reali coincidenti in x=0 → y=0. Il grafico della corrispondente funzione y=ax2 è tangente all'asse x nell'origine
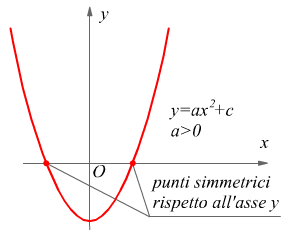
Equazione pura
![]()
se ha soluzioni, sono due soluzioni opposte. Il grafico della corrispondente funzione y=ax2+c se interseca l'asse x, lo interseca in due punti simmetrici rispetto all'asse y.
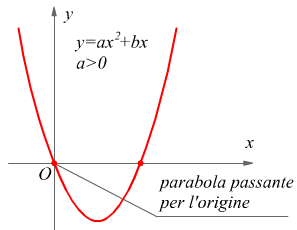
Equazione spuria
![]()
Una delle due soluzioni è sempre zero, quindi, uno dei due punti di intersezione del grafico della funzione y=ax2+bx con l'asse x è sempre l'origine.
In base a queste constatazioni si intuisce come le coordinate del vertice di una parabola possono essere ricavate basandosi sulle eventuali radici del trinomio di secondo grado ax2+bx+c.
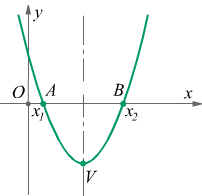
Ipotizziamo una parabola che intersechi l'asse x nei due punti A(x1,0)
e B(x2,0) indichiamo poi con V(xv,yv) il
suo vertice.
L'asse della parabola è la retta verticale passante per il vertice e quindi
ha equazione x=xv.
Dal momento che la parabola è simmetrica rispetto al suo asse, il punto medio di AB deve appartenere a tale asse, perciò deve essere.
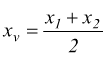
D'altra parte sappiamo che x1 e x2 sono gli zeri (radici) della funzione, cioè le soluzioni dell'equazione ax2+bx+c=0
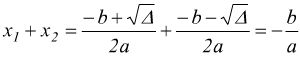 si
ha
si
ha
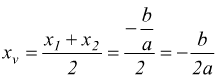
l'ordinata del vertice si può ottenere sostituendo xv nell'equazione della parabola
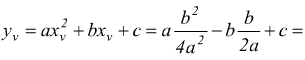
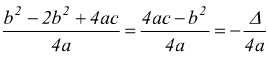
si conferma che le coordinate del vertice sono 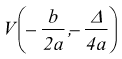
ma la coordinata yv è più comoda da calcolare come 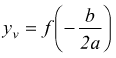 cioè
inserendo la coordinata xv nell'equazione y=ax2+bx+c.
cioè
inserendo la coordinata xv nell'equazione y=ax2+bx+c.
Tangenti ad una parabola
E' possibile riconoscere se una retta è tangente ad una parabola, basta risolvere il sistema di secondo grado in x e in y formato dall'equazione della retta e dall'equazione della parabola
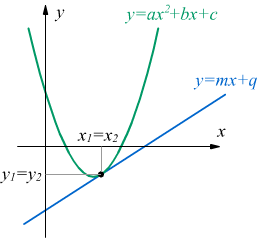
se il sistema ha due soluzioni (x1,y1)≡(x2,y2)
coincidenti allora la retta e la parabola sono tangenti.
Questo può accadere se l'equazione di secondo
grado risultante ha discriminante nullo.
Alle due soluzioni coincidenti del sistema corrisponde l'unico punto di
intersezione tra la retta e la parabola, cioè il punto di tangenza (o punto
di contatto).
Tangenti ad una parabola da un punto esterno
In questo tipo di problema viene richiesto di identificare le rette tangenti ad una parabola passanti per un punto esterno ad essa che chiamiamo P(xo,yo). E' noto che da un generico punto disposto su un piano passano infinite rette descritte dall'equazione di un fascio di rette passanti per il punto assegnato
![]()
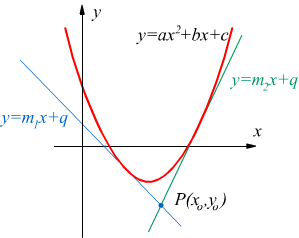
al variare del coefficiente angolare m si hanno infinite rette, soltanto due di queste infinite rette potranno essere quelle tangenti alla parabola data.
Per determinare i coefficienti angolari m1 ed m2 delle due tangenti facciamo il sistema tra l'equazione della retta generica passante per P(xo,yo) con l'equazione della parabola
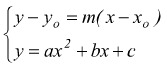
applicando il metodo di sostituzione, si elimina la y ottenendo un'equazione
di secondo grado in x che chiamiamo 'risolvente'.
I coefficienti di quest'ultima equazione saranno funzioni del parametro
m mentre le soluzioni dell'equazione risolvente se esistono sono le ascisse
dei punti di intersezione tra la retta passante per P e la parabola.
Affinché la generica retta passante per P sia tangente alla conica occorre
che l'equazione risolvente ammetta due soluzioni coincidenti cioè che abbia
discriminante nullo (Δ=0)
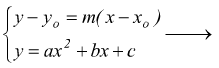
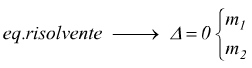
In tal modo si ottengono proprio i due coefficienti m1 ed m2 cercati che sostituiti nel fascio di rette forniscono
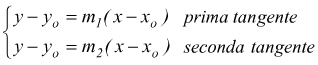
 edutecnica
edutecnica