Disequazioni irrazionali
Una disequazione si dice irrazionale, quando in essa compaiono uno o
più radicali contenenti l'incognita.
Per la sua soluzione, si cerca, ovviamente, in prima istanza, di portarla
in forma razionale; per consuetudine si applica il principio di elevamento
a potenza di entrambi i membri della disequazione.
Consideriamo le due disequazioni:
![]()
se n è dispari si trasformano immediatamente in
![]()
Esempio:
![]() Verificata
per x<3 o per x>5
Verificata
per x<3 o per x>5
Consideriamo n pari con la seguente coppia di disequazioni:
![]()
Per verificare la prima ![]() deve
risultare per il radicando
deve
risultare per il radicando ![]() conseguentemente
deve essere verificata la
conseguentemente
deve essere verificata la ![]() ed
infine si dovrà avere:
ed
infine si dovrà avere: ![]() in
pratica la soluzione della disequazione coincide con la soluzione del
sistema:
in
pratica la soluzione della disequazione coincide con la soluzione del
sistema:
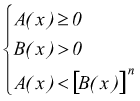
Esempio: ![]() risulta
equivalente al sistema:
risulta
equivalente al sistema:
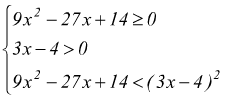 cioè
cioè 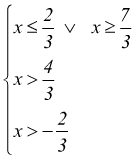
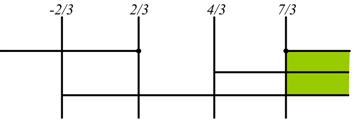 la disequazione è verificata per
la disequazione è verificata per ![]()
Se risulta invece ![]() è
possibile che la relazione sia verificata sia quando
è
possibile che la relazione sia verificata sia quando ![]() e
e ![]()
oppure quando ![]() ed
ed ![]()
Le soluzioni della disequazione, sono, in questo caso, tanto quelle dell'uno quanto quelle dell'altro, di uno dei seguenti due sistemi:
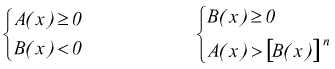
Esempio:
![]() avremo,
per quanto si è detto:
avremo,
per quanto si è detto:
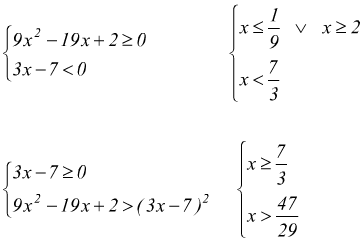
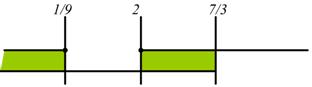 Il
primo sistema è verificato per
Il
primo sistema è verificato per 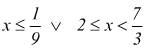
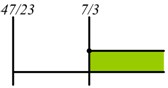 Il
secondo sistema e verificato per
Il
secondo sistema e verificato per ![]()
Dato che tutti e due i sistemi sono soluzione della disequazione, noi
prenderemo l'unione
delle soluzioni dei due sistemi cioè: ![]() dunque:
dunque: ![]()