Disposizioni
Dato l’insieme A=[a,b,c,d] scrivere tutte le sigle di due elementi che si possono formare con gli elementi di A.
| aa | ab | ac | ad |
| ba | bb | bc | bd |
| ca | cb | cc | cd |
| da | db | dc | dd |
Questi raggruppamenti sono detti disposizioni con ripetizione di 4 elementi in classe
2 essi sono 42=16.
Classe 2, significa che ogni raggruppamento
è costituito da 2 elementi.
per formare le disposizioni di classe 3 a ciascuno degli elementi precedenti bisogna associare un elemento dell’insieme A=[a,b,c,d]
| aaa | aab | aac | aad |
| aba | abb | abc | abd |
| … | ... | ... | ... |
| dda | ddb | ddc | ddd |
in totale si avranno 43=64 raggruppamenti
Disposizioni semplici (senza ripetizione)
|
|
ab | ac | ad |
| ba |
|
bc | bd |
| ca | cb |
|
cd |
| da | db | dc |
|
Dato lo stesso insieme A=[a,b,c,d] costruiamo
i raggruppamenti formati da 2
elementi diversi; che sono in numero di 4×3=12.
I raggruppamenti di questo tipo vengono detti disposizioni
semplici di 4 elementi di classe 2.
Le disposizioni semplici di classe 3 si ottengono associando ad ogni raggruppamento precedente un diverso elemento di A.
| abc | abd |
| acb | acd |
| ... | ... |
| dba | dbc |
| dca | dcb |
Poiché i raggruppamenti precedenti erano 4×3=12 e da ognuno di essi se ne ottengono altri 2, in totale il numero di disposizioni semplici di 4 elementi in classe di classe 3 è 4×3×2=24.
Dato un insieme di n elementi si definisce disposizione di classe k, i raggruppamenti di k elementi scelti tra gli n dell’insieme tali che ogni raggruppamento differisca dagli altri o per la natura degli elementi o per l’ordine degli elementi.
Le disposizioni sono con ripetizione se nei raggruppamenti gli elementi di A possono comparire più di una volta:
![]() disposizioni
con ripetizione
disposizioni
con ripetizione
Le disposizioni si dicono semplici se ogni raggruppamento contiene elementi distinti fra loro
![]() disposizioni semplici
disposizioni semplici
In questa pagina un calcolatore rapido di disposizioni.
Esempi di diagrammi ad albero
Disposizione con ripetizione di 3 elementi in classe 2
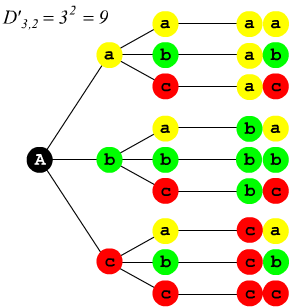
Disposizione semplici di 3 elementi in classe 2
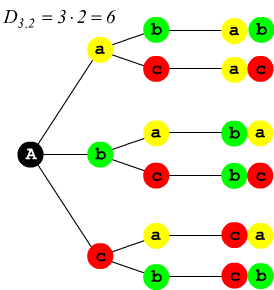
Dato l'insieme di cifre A=[1, 2, 3, 4, 5] quanti numeri di due cifre si
possono formare se le cifre non possono essere ripetute?
In questo caso si tratta di calcolare le disposizioni di 5 elementi in classe
2.
![]()
le disposizioni sono le seguenti
| 12 | 13 | 14 | 15 |
| 21 | 31 | 41 | 51 |
| 23 | 24 | 25 |
| 32 | 42 | 52 |
| 34 | 35 |
| 43 | 53 |
| 12 |
| 21 |
Come si può constatare tutti questi numeri differiscono tra loro per
almeno una cifra (sulle righe) o per l'ordine
con cui le cifre possono essere prese (sulle colonne).
Si noti che questo problema è equivalente al seguente: quanti e quali sono
gli elementi dell'insieme dell'esperimento che consiste nell'estrarre, senza
reintroduzione, 2 palline da un'urna che ne contiene 5 (numerate
da 1 a 5).
 edutecnica
edutecnica