Rotolamento
Consideriamo una ruota di raggio r che rotola senza strisciare su una superficie rettilinea, piana, liscia e priva di attriti.
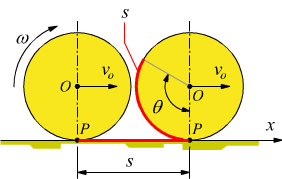
In un dato intervallo di tempo, sia il centro di massa O che il punto di contatto P, tra la ruota e la superficie si postano orizzontalmente di un tratto s, in concomitanza di una rotazione θ della ruota stessa. Per la geometria:
la velocità media del centro di massa O e del punto di contatto P in direzione x sarà:
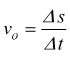mentre
per la velocità istantanea del centro di massa
avremo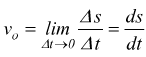 
[
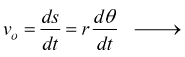
m/s ] ✘
Il moto di rototraslazione (rotolamento) può essere interpretato come la combinazione dei due moti di traslazione e di rotazione.
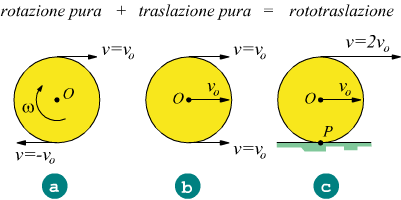
Nel caso a abbiamo un moto di pura rotazione, con asse di rotazione stazionario passante per il centro di massa, il punto più alto della ruota possiede velocità periferica v pari a quello trovato nell'equazione ✘; il punto più basso ha velocità uguale ed opposta.
Nel caso b si ha la traslazione pura e nessun tipo di rotazione, in tal caso ogni punto della ruota si muove in direzione x con la stessa velocità del centro di massa vo.
Nel caso c si ha la combinazione dei due moti precedenti con il punto P di contatto alla superficie che rimane fisso costituendo un fulcro per l'intera ruota che vede il centro di massa muoversi sempre con velocitò vo mentre il punto più alto si muove al doppio (2vo) di tale velocità.
Energia cinetica
Il moto di rotolamento può dunque essere interpretato come un moto di rotazione attorno al punto di contatto P.
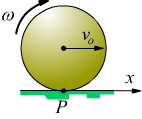
l'energia cinetica vale in tal caso 
Jp momento di inerzia rispetto al punto di rotazione P. Poi
per il teorema degli assi paralleli di Huygens: 
;
con Jo momento di inerzia relativo all'asse passante per
il centro di massa della ruota. Sostituendo:
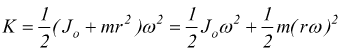in
definitiva
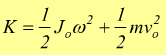
La formula del momento di inerzia per i principali tipi di solidi è
riportato in questa tabella.
Nel moto di rototraslazione si hanno due tipi di energia cinetica: un'energia
cinetica di rotazione dovuta alla rotazione del corpo rigido attorno al
suo cento di massa e un'energia cinetica traslazionale riconducibile alla
traslazione del suo centro di massa, come avevamo già accennato nel
caso dell'atto
di moto rotatorio.
Se la ruota accelera sempre senza strisciare, l'accelerazione del centro di massa ao è in relazione con l'accelerazione angolare α attorno al suo centro, secondo la formula
Consideriamo, ora, una ruota che rotola senza slittare in discesa lungo un piano inclinato. La sua forza peso p=mg può essere decomposta nelle due componenti parallela pt e normale pn al piano inclinato. La componente normale pn viene compensata dalla reazione vincolare di appoggio al piano V.
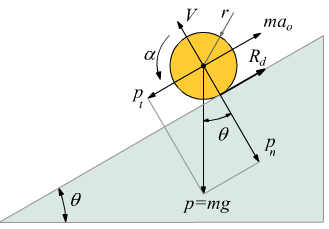
La componente parallela al piano pt=mg·sinθ determina il moto di rotolamento. Lungo la direzione tangente al piano avremo allora:
per la legge di Newton in forma rotazionale deve essere anche
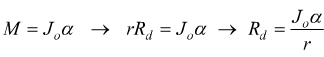
con r raggio della ruota e Rd attrito dinamico volvente di rotolamento che costituisce la forza associata al momento M. Sostituendo
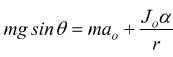con
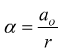
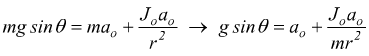
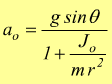
si ha l'accelerazione del centro di massa di una ruota ruota che rotola senza slittare lungo una rampa inclinata lungo la direzione parallela al piano inclinato.