Distribuzione chi-quadro
Oltre alla distribuzione normale, esistono altre distribuzioni di probabilità
molto interessanti per vari settori di applicazione, una di queste è la
distribuzione chi-quadro indicata χ
introdotta da K.Pearson.
Si considerano ν (pron. nu) variabili aleatorie indipendenti Y1,Y2,..Yν
distribuite secondo la legge normale con media μ=0
e varianza σ2=1; allora la variabile
χ2 è:
Si tratta di una distribuzione, chiamata distribuzione chi-quadro, con ν gradi di libertà. Le proprietà fondamentali della distribuzione chi-quadro sono:
1) Asimmetria.
2) Dipendenza dal parametro intero ν che indica
i gradi di libertà: per ogni valore di ν si ha
una curva diversa.
3) La variabile χ2 non può assumere
valori negativi dato che è una somma di quadrati
4) E' completamente definita nel primo quadrante.
L'andamento di χ2 per vari valori di ν è indicato nel disegno.
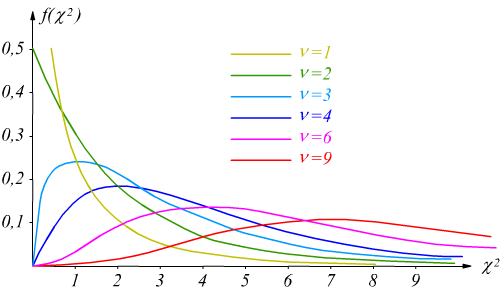
Come per tutte le distribuzioni di probabilità, l'area compresa tra ogni curva e l'asse delle ascisse è uguale ad 1.
La distribuzione chi-quadro è additiva, cioè se Y1 ed Y2 sono due variabili indipendenti con distribuzione chi-quadro aventi rispettivamente ν1 e ν2 gradi di libertà, la variabile
è ancora una variabile con distribuzione chi-quadro ed ha
Formalmente il simbolo usato per indicare una distribuzione χ2 è il seguente
in modo da sintetizzare il numero di gradi di libertà ed il percentile usato.
I valori critici della coda superiore e della coda inferiore della distribuzione chi-quadro sono contenuti nella seguente tabella.
Esempio: Determinare il valore
di 
con
5 gradi di libertà
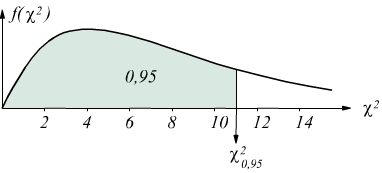In
questo caso si deve trovare il valore di χ2
per cui il 95%dell'area sotto la curva si trovi alla sinistra di una ordinata
innalzata da questo valore e il 5% (0,05) a destra per 5 gradi di libertà.
Dalla tabella, nella riga corrispondente a 5 gradi di libertà per un
valore di 1-p=0,05 si ottiene :
bisogna precisare che, in questo caso, 0,95 è il valore della funzione di ripartizione corrispondente a χ2=11,07 con 5 gradi di libertà; si può quindi dire che
Distribuzione di Student
Oltre alla distribuzione chi-quadro esiste un'altra distribuzione importante:
la distribuzione di Student, elaborata
da W.S. Gosset che ha elaborato la teoria, appunto, sotto lo pseudonimo
di Student.
Per descriverla basta ipotizzare due variabili casuali indipendenti
– Z: distribuita normalmente con media μ=0
e varianza σ=1
– Y:distribuita secondo chi-quadro con ν
gradi di libertà.
E' possibile affermare che
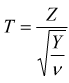La
distribuzione di T è una distribuzione di Student con ν
gradi di libertà.
Le caratteristiche di questa distribuzione sono:
– Simmetria rispetto al valor medio μ=0;.
– Dipendenza dal parametro ν gradi di libertà.
– Tende alla distribuzione normale quando ν
tende ad infinito (ν ⟶ ∞).
– Per ogni valore di ν si ha una diversa
distribuzione.
– Come nel caso della normale, l'area compresa tra la curva e l'asse
delle ascisse vale 1.
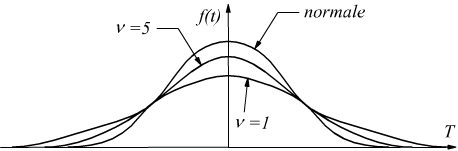
Tabella della distribuzione t di Student per P(T<t)=p
Esempio: determinare per quale valore di t è valida la relazione P(T ≤ t)=0,90 con 6 gradi di libertà.
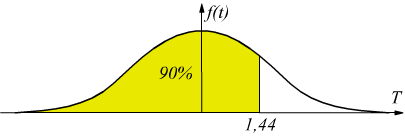
Dalla tavola con ν=6 gradi di libertà si va nella colonna contrassegnata 0,9 e alla riga 6 trovando t=1,44
Esempio: determinare per quale valore di t è valida l'uguaglianza P( -t <T< t )=0,95 con 7 gradi di libertà .
L'area totale sottesa alla curva di funzione vale 1. In questo caso si considera il 95% dell'area sottesa alla curva e simmetrica rispetto l'asse delle ordinate e più precisamente si cercano i corrispondenti valori di t, associati.
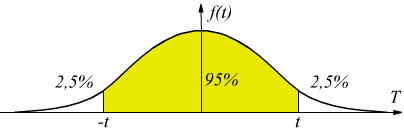come
si vede dal disegno, nella coda di destra rimane libero il 2,5% dell'area.
Se ci rifacciamo alla tabella, per come sono rappresentati i dati, il
valore cercato di t deve corrispondere a quello per il quale si ha p=1-0,025=0,975
cioè t=2,365