Distribuzione binomiale
E' detta anche distribuzione di Bernoulli, è la
più importante fra le distribuzioni discrete e definisce la distribuzione
di probabilità di n prove ripetute e indipendenti, quando i risultati possibili
di ciascuna prova possono essere soltanto due: il successo :
p : probabilità
.favorevole all'evento
e l'insuccesso
q=1-p :
probabilità sfavorevole all'evento.
Prove dipendenti sono ad esempio le estrazioni ripetute senza reintroduzione come nel caso del gioco del lotto dove la variabile aleatoria non mantiene la stessa probabilità di successo. Prove indipendenti sono eventi che non dipendono dalla storia precedente, ad esempio il lancio di un dado o l'estrazione di un numero alla roulette dove la variabile aleatoria conserva sempre la stessa probabilità di successo.
La distribuzione binomiale è la probabilità di ottenere x successi in n prove indipendenti.
Questa probabilità è data da:
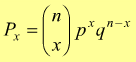 con
0 ≤ x ≤ n
con
0 ≤ x ≤ n
Questa è la distribuzione binomiale o di Bernoulli a parametri
n e p.
Esempio: Si lancia lancia un dado, n=4 volte studiare la variabile binomiale
x=numero di volte in cui è uscito un numero <=2 quindi:
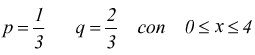
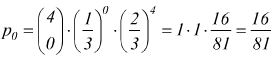 probabilità
che x non esca neanche una volta
probabilità
che x non esca neanche una volta
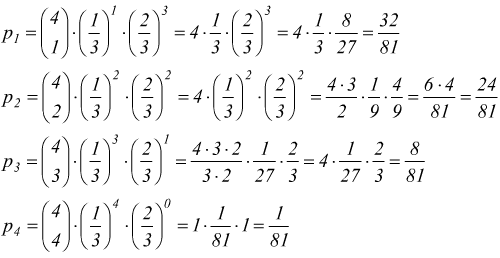
il grafico della distribuzione di probabilità
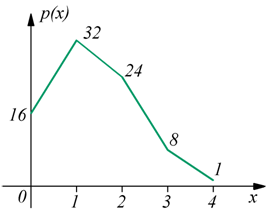
Esempio:
Una moneta è lanciata n=7 volte, studiare la distribuzione di probabilità
della variabile binomiale x= numero di volte in cui compare testa
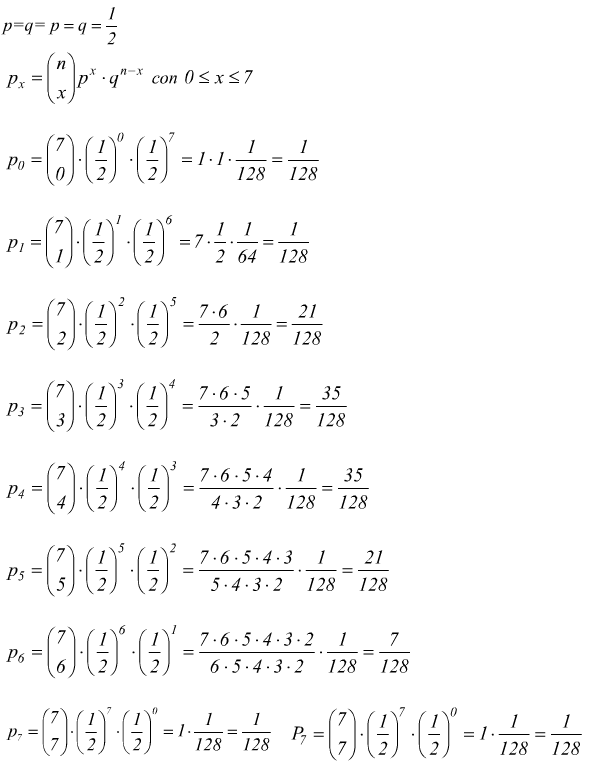
dai valori ottenuti otteniamo il grafico della distribuzione

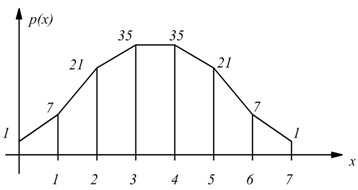
il grafico della funzione di ripartizione è il seguente:
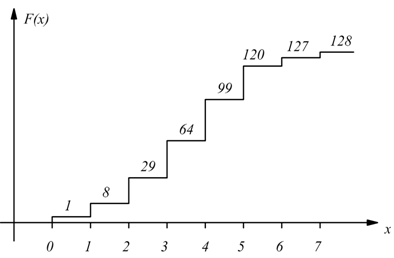
Per la distribuzione binomiale valgono le seguenti formule:
![]() valor
medio
valor
medio
![]() varianza
varianza
Esempio: in una officina sono installate 5 macchine uguali, ciascuna ha probabilità del 20% di guastarsi, studiare la variabile casuale X=numero di macchine guaste simultaneamente.
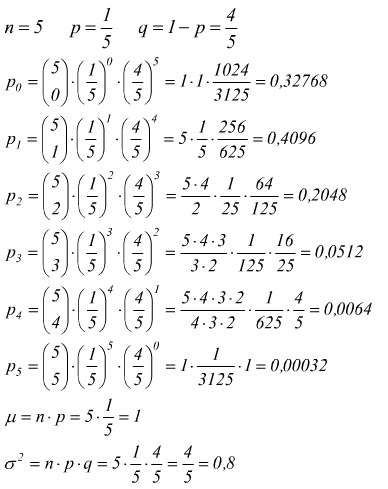
Se si vogliono usare i numeri con la virgola, i calcoli possono
essere verificati nel modo seguente:
p
n
k
Infatti si verifica che:
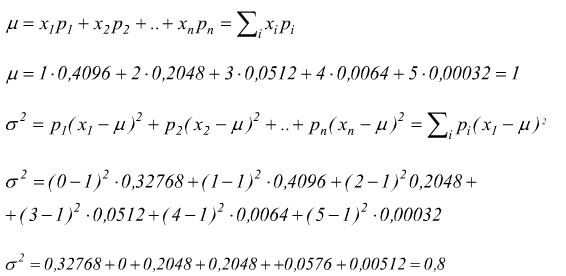
..come preventivato
esempio: lancio di una moneta per n=6 volte; studiare la variabile aleatoria
x=numero di volte in cui appare testa. Facendo i calcoli:

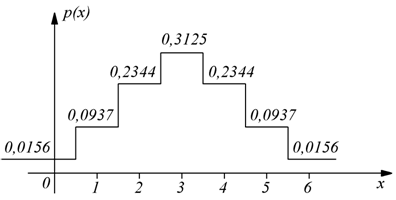
stavolta rappresentiamo la distribuzione di probabilità tramite
un grafico a gradini: anche in questo caso potremmo constatare:
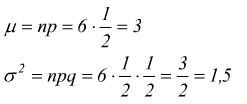
esempio: lancio di una moneta per n=12 volte; studiare la variabile
aleatoria x=numero di volte in cui appare testa. facendo i calcoli:

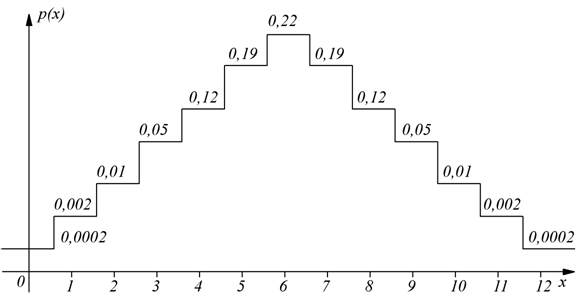
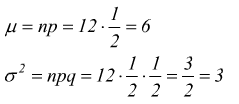
in entrambi i casi n=6 ed n=12 l'area sottesa alla spezzata vale
1. Automatizzando la procedura:
n
p
maggiore di
minore di
compreso tra
e
inclusi
probabilità ►
In ogni caso, si ottiene un istogramma o meglio, una spezzata che può
essere approssimata alla funzione
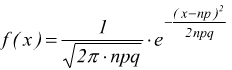
considerando che ![]() e che
e che ![]()
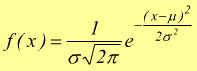
funzione di densità di probabilità della distribuzione
normale di media μ=6 e varianza σ2= 2.
La distribuzione è esempre disposta attorno al valor medio .
Nel caso p=q la distribuzione è simmetrica.
Valore medio (speranza matematica)
Il parametro che permette di definire la zona di massima probabilità di una variabile aleatoria è la media μ che si ottiene moltiplicando tutti i valori della variabile per le rispettive probabilità.
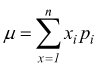 per
dimostrare che μ=n·p sostituiamo:
per
dimostrare che μ=n·p sostituiamo:
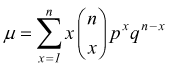 sapendo
che
sapendo
che 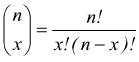 si
ha
si
ha
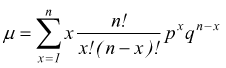 ricordando
che
ricordando
che 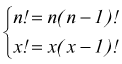
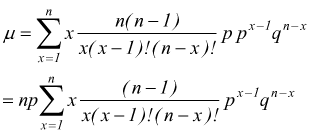
ponendo m=n-1 e k=x-1 → m-n=k-x → n-x=m-k
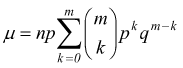 per
le proprietà dei coefficienti binomiali
per
le proprietà dei coefficienti binomiali
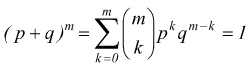 perché
p+q=1 quindi è μ=n·p
perché
p+q=1 quindi è μ=n·p
Varianza
Per definizione è 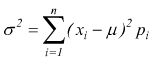 dove
xi-μ sono gli scarti associati ad ogni singolo valore della
variabile aleatoria X; dopo qualche passaggio si ottiene:
dove
xi-μ sono gli scarti associati ad ogni singolo valore della
variabile aleatoria X; dopo qualche passaggio si ottiene:
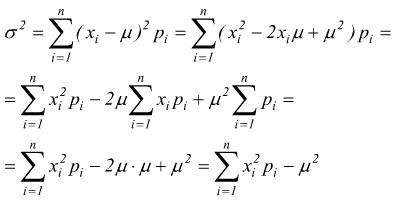
ma il termine 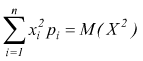 è
la media dei valori della variabile aleatoria X elevati al quadrato; dunque:
σ2=M(X2)-μ2 . Sostituendo pi
con il valore rappresentato nell'equazione di Bernoulli:
è
la media dei valori della variabile aleatoria X elevati al quadrato; dunque:
σ2=M(X2)-μ2 . Sostituendo pi
con il valore rappresentato nell'equazione di Bernoulli:
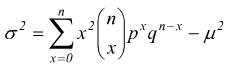 artificio:
si pone x2=x(x-1)+x quindi
artificio:
si pone x2=x(x-1)+x quindi
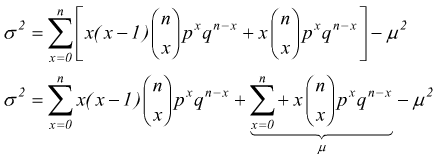
dunque
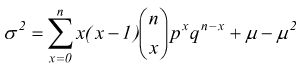 se
si svolge il coefficiente binomiale.
se
si svolge il coefficiente binomiale.
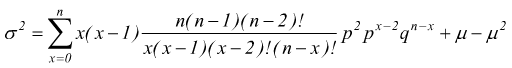
ponendo k=x-2 ed m=n-2 ricordando le proprietà dei coefficienti binomiali
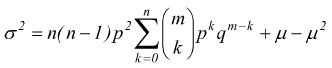
ma 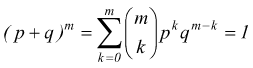 ne
consegue
ne
consegue
![]() avendo
già dimostrato che μ=np , quindi
avendo
già dimostrato che μ=np , quindi
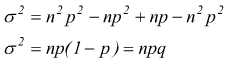
 edutecnica
edutecnica