Funzione di trasferimento di sistemi meccanici
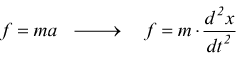
Per la legge di Newton della Fisica classica, è noto che un corpo, inizialmente fermo, sotto l'effetto di una forza f(t) variabile nel tempo (in assenza di attriti) subisce un'accelerazione e si mette in moto con velocità v(t).
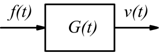
Esiste un legame fra la sollecitazione ( la causa forzante ) f(t)
e la risposta del sistema costituito dalla velocità; noi vorremmo trovare
questo legame. Rappresentato con lo schema a blocchi sopra disegnato,
questo legame è dato dalla funzione di trasferimento G(t).
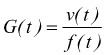
Per la legge di Newton ( II legge della Dinamica ) dunque:
![]() poi
poi 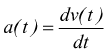 quindi
quindi 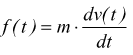
Si nota che in questo tipo di problemi la conclusione è sempre una equazione
integro-differenziale più o meno articolata e più o meno difficile da
risolvere.
Per ragioni di comodità di calcolo, talvolta, si preferisce usare un approccio
attraverso la trasformata di Laplace; per il teorema III qui
visto :
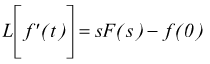
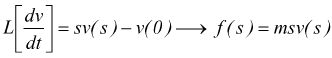
è stata fatta l'ipotesi che il corpo fosse inizialmente fermo. Si ricava:
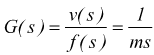
G(s) è la funzione di trasferimento del sistema.
Nota la f.d.t. la risposta v(t) del sistema dipende esclusivamente
dalla forza in ingresso, se ipotizziamo che questa sia costante:
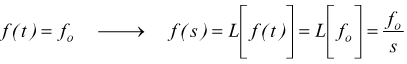 avremo
di conseguenza
avremo
di conseguenza
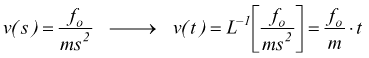
se invece di studiare il legame fra forza applicata e velocità ci interessa avere come variabile di uscita la posizione x (spostamento) dell'oggetto considerato
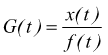 si
ha
si
ha ![]() e
anche
e
anche
![]()
torniamo alla seconda legge della Dinamica
 sempre
per il teorema III di Laplace
sempre
per il teorema III di Laplace
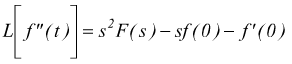 applicata
allo spostamento x
applicata
allo spostamento x
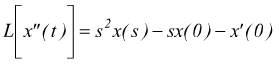
se ipotizziamo che la posizione iniziale sia x=0 e che la velocità iniziale sia nulla x'=0
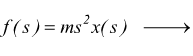
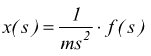
con
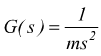
anche in questo caso, per semplicità, pensiamo di applicare una forza costante; risulterà essere
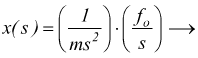
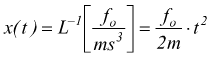
quest'ultima coincide, ovviamente, con la 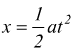 della
Fisica classica, ottenuta coi metodi dell'Analisi Matematica.
della
Fisica classica, ottenuta coi metodi dell'Analisi Matematica.
La presenza di dell'attrito viscoso si caratterizza in Meccanica con una forza resistente
![]() (
negativa perché si oppone alla direzione della forza agente f )
(
negativa perché si oppone alla direzione della forza agente f )
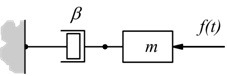
con β=coefficiente di attrito viscoso mentre v=velocità;
il principio di D'Alembert afferma:
m·a=forze attive + forze resistenti
![]()
supponiamo di voler determinare la velocità mantenendo la forza come variabile di ingresso.
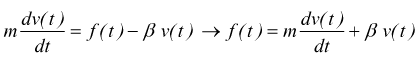
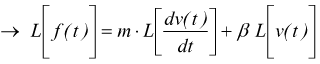
mantenendo le stesse ipotesi sulle condizioni iniziali ( per t=0 ) con f(t)=fo.
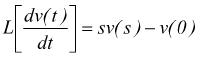 mentre
mentre 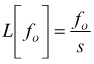
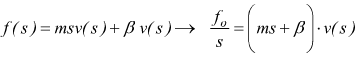
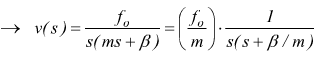
dalla tabella delle trasformate si ha
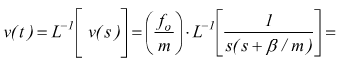
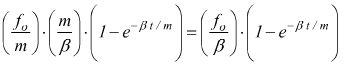

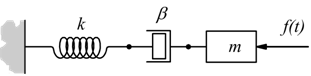
Oscillatore armonico
E' il caso delle vibrazioni forzate di una molla già viste, dove il principio di D'Alembert viene scritto come
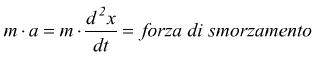
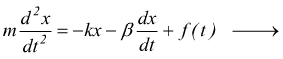
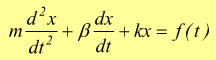
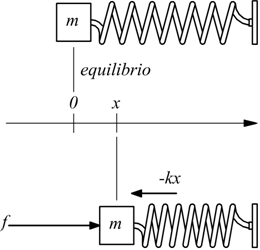
supponiamo di voler stabilire la relazione fra velocità e forza senza che vi sia smorzamento β.
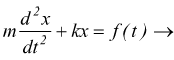
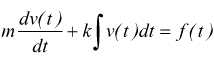
Dai teoremi sulla trasformata sappiamo che se
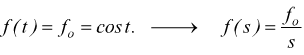
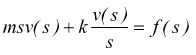 la
funzione di trasferimento
la
funzione di trasferimento 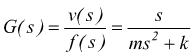
poi sostituendo la f(s)
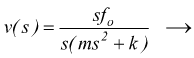
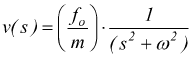
con
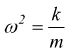
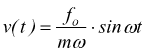
Oscillatore smorzato
Il caso delle oscillazioni smorzate è già stato valutato nel caso della molla
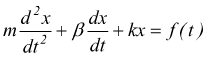 con
le stesse valutazioni fatte prima avremo
con
le stesse valutazioni fatte prima avremo
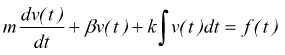
nel campo della variabile complessa s:
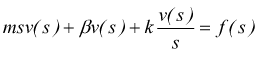
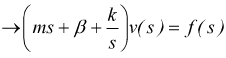
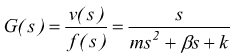 anche
in questo caso se
anche
in questo caso se 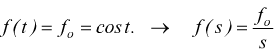
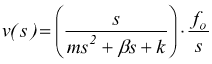
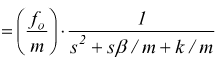
la risposta nel tempo dipende dalle radici del trinomio al denominatore; se ammettiamo due radici reali distinte a e b si può applicare la formula dalla tabella:
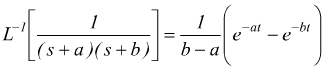
Se le radici sono reali coincidenti pari ad a, si applica la
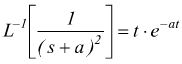
altrimenti si applica la
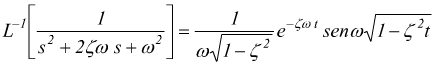
con 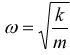 e
e 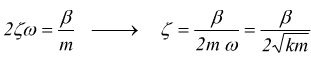 si
nota inoltre
si
nota inoltre
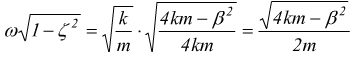 e
e 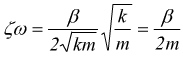 quindi
quindi
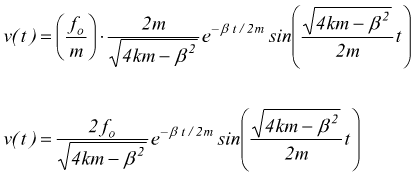
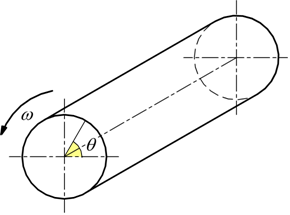
Moto rotatorio
In Meccanica applicata, è il problema di un albero soggetto ad una coppia
che deve essere trasmessa.
I Fisici preferiscono parlare di un cilindro in rotazione di momento di
inerzia pari a J sotto l'azione di una coppia C che nella
letteratura può anche essere chiamata MT ( momento torcente
) o τ ; con θ viene indicato l'angolo formato
con un asse convenzionale mentre ω è la velocità angolare.
E' dimostrato
che risulta:
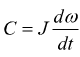 o
meglio
o
meglio 
applicando il teorema III di Laplace
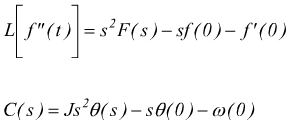
imponendo come condizioni iniziali θ(0)=0 e ω(0)=0
si ha ![]()
la funzione di trasferimento fra lo spostamento angolare θ e la coppia è
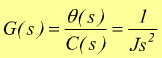
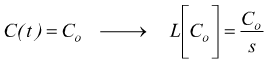
se si vuole trovare la risposta nel dominio del tempo, basta antitrasformare. Nell'ipotesi che il sistema sia soggetto alla coppia costante Co con
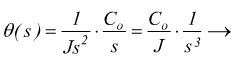
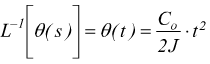
in presenza di attrito viscoso, la coppia deve bilanciare anche quest'ultimo
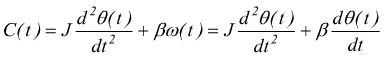 di
conseguenza
di
conseguenza
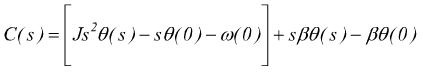 con
le stesse condizioni iniziali di prima
con
le stesse condizioni iniziali di prima
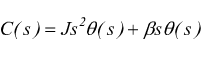
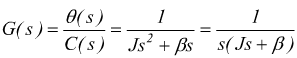
Il coefficiente di attrito β deve essere dimensionalmente compatibile con l'equazione impostata; se stiamo facendo un bilancio di forze si parla di [Kg/s] o [Ns/m] ; se si tratta di un bilancio di coppie ( come in questo caso ) si ha [Nm2/s].
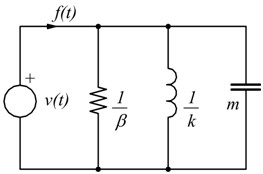
Schemi elettrici equivalenti
Si intuisce che il comportamento di sistemi meccanici può essere ricondotto a schemi elettrici per essere in questo modo più facilmente studiato; bisogna riassumere il comportamento dei vari componenti elettrici nel dominio della variabile complessa s di Laplace.
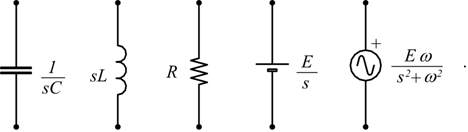
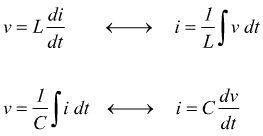
Gli ultimi due componenti a destra, sono rispettivamente un generatore di tensione costante di valore E ed un tradizionale generatore in alternata di valore E·sinωt.
Per il generico oscillatore si avrebbe
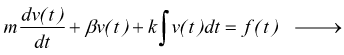
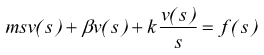
facciamo corrispondere la forza applicata alla tensione e la velocità alla corrente se si vuole il circuito serie; oppure il contrario se si vuole fare il circuito parallelo.
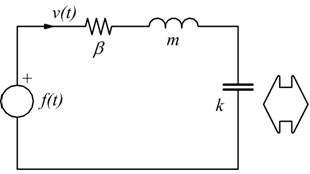
 edutecnica
edutecnica