Conversione binario - decimale
Il sistema numerico binario è un sistema numerico usato nei calcolatori elettronici; è a base due, vengono infatti usate soltanto due cifre:0 e 1, indicate usualmente col termine di bit (binary digit=cifra binaria) per formare il numero binario in questione. Un qualsiasi numero nel sistema binario può essere rappresentato da una serie di bit equivalente ad una somma di potenze del due ognuna delle quali moltiplicata per una cifra che può essere solo 0 o 1. In questo modo le scritta (1111)2 e (111,01)2 devono interpretate come:
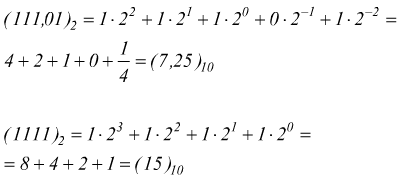
nel caso in cui il numero binario abbia degli zeri supplementari sulla sinistra,
questi vanno ignorati:
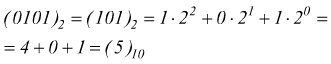
Conversione decimale - binario
Per questo tipo di conversione si ricorre ad un metodo che implica la divisione
ripetuta per due del numero assegnato.
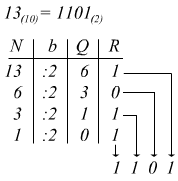
Volendo convertire il numero 12:
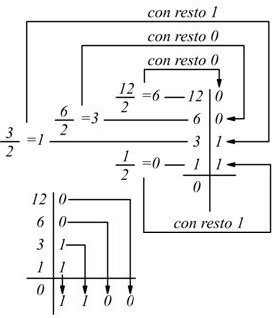
infatti: (1100)2 = 1×23+1×22+0×21+0×20 = 8+4+0+0 = (12)10 in conseguenza degli esempi riportati è facile ottenere la corrispondenza fra i numeri del sistema binario a 4 bit e i corrispondenti valori del sistema decimale:
| base 2 BIN |
base 10 DEC |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
Conversione esadecimale - decimale
Il sistema numerico esadecimale è un sistema a base 16, perchè i numeri che si possono rappresentare sono sedici:le cifre che vanno da 0 a 9 non sono più sufficienti, di conseguenza si usano anche le prime 6 lettere dell’alfabeto; i sedici simboli sono:
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
Per il precedente schema A=10; B=11; C=12; D=13; E=14;F=15.
Ciascun numero del sistema esadecimale può essere espresso come somma delle
potenze del 16, ognuna delle quali moltiplicata per il valore di ciascuno
dei 16 simboli suddetti.
(1BC)16 = 1×162+11×161+12×160 = 256+176+12 = (444)10
(FFF)16 = 15×162+15×161+15×160 = 3840+240+15 = (4095)10
(123)16 = 1×162+2×161+3×160 = 256+32+3 = (291)10
Conversione decimale - esadecimale
Si effettua nello stesso modo della conversione decimale-binario considerando
che in questo caso la base è 16.
Ad es. volendo convertire 177 in base 10 nel corrispondente numero
esadecimale:
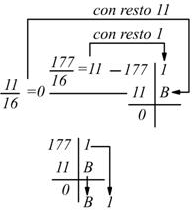
infatti: (B1)16=11×161+1×160 =176+1 =(177)10
altro esempio su come si eseguono i passaggi, convertendo (946)10 in esadecimale:
In alternativa al metodo precedente, la conversione decimale binario può essere facilmente automatizzata da un algoritmo più strutturato che preveda di inquadrare in una tabella i risultati delle divisioni successive per 2 valutando quoto Q e resto R di per ciascuna di queste.
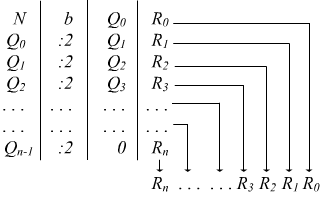
1 Dividiamo il numero decimale N per la base
2 otteniamo un quoziente Q0 e un resto R0 .
Il resto sarà il bit meno significativo LSB (Least Significant Bit) del
numero cercato; se R0=0 il numero è pari, se R0=1
il numero è dispari.
2 Dividiamo il quoziente Q0 ancora per ; otterremo ancora un nuovo quoziente Q1 con resto R1.
3 Continuiamo questo procedimento finché Q=0
.
A questo punto il numero binario si ottiene posizionando orizzontalmente
i resti delle divisioni con R0 LSB ed Rn MSB (Most
Significant Bit). Ad esempio:
I metodi esposti per le conversioni numeriche decimale - binario - esadecimale possono essere generalizzati a qualsiasi base.
Conversione di un numero da base b a base 10
La conversione da base b a base 10 è immediata. Basta ricordare che un numero in base b è rappresentato da una sequenza di cifre del tipo
![]() con
con
![]()
questa sequenza, in notazione posizionale, significa che il corrispondente numero in notazione decimale Nd può essere scritto come
![]()
vediamo alcuni esempi con numeri interi
Convertire il numero in codice ottale 143(8) in base 10
![]()
Convertire il numero in codice esadecimale AD2(16) in base 10
![]()
nel caso il numero non sia intero bisogna tener presente che dopo la virgola vi saranno cifre espresse con la base in potenze decrescenti.
Convertiamo 37,61(8) in base 10
![]()
Convertiamo B,2F(16) in base 10
![]()
Convertiamo il numero binario 1,011(2) in base 10
![]()
Conversione di un numero da base 10 a base b
Per convertire un numero intero da base 10 ad una base qualsiasi, si procede,
come abbiamo visto, utilizzando una procedure di divisioni successive per
la base di destinazione desiderata, ottenendo il risultato considerando
la sequenza dei resti in ordine inverso al loro ottenimento.
Possiamo fare un esempio ulteriore convertendo 275(10) in base
8 con questo secondo schema illustrato.
 cioè
275(10)=432(8)
cioè
275(10)=432(8)
Convertire 2876(10) in base 16
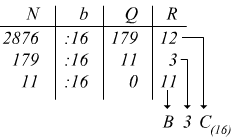 cioè
2876(10) = B3C(16)
cioè
2876(10) = B3C(16)
L'algoritmo di conversione di un numero minore di 1 (<1) da base 10 ad una base b qualsiasi utilizza un procedimento basato su moltiplicazioni successive, dove otteniamo un prodotto (P) di cui dobbiamo considerare la parte intera (PI) e la parte frazionaria (P-PI).
Convertire 0,4375(10) in base 2
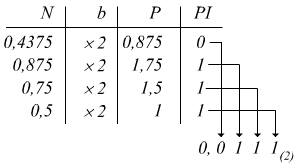 dunque
0,4375(10) = 0,1111(2)
dunque
0,4375(10) = 0,1111(2)
Convertire 0,2890625(10) in base 16
 0,2890625(10)
= 0,4A(16) in base 16
0,2890625(10)
= 0,4A(16) in base 16
Convertiamo il numero 0,3(10) in base 2
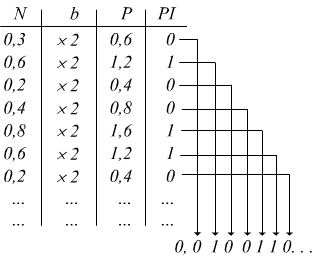
in questo caso il risultato è periodico perchè la parte frazionaria P-PI non si annulla mai e risulta
0,3(10) = 0,01001(2) in base 2
Per un numero positivo qualsiasi, cioè, quando il numero decimale si presenta completo di parte intera e parte frazionaria, lo si suddivide eseguendo separatamente gli algoritmi relativi. Convertiamo 101,25(10) in base 8
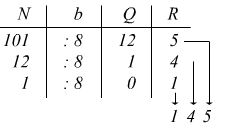
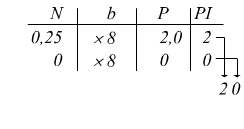 cioè
101,25(10)=145,20(8)
cioè
101,25(10)=145,20(8)
Convertire 55,125(10) in base 2
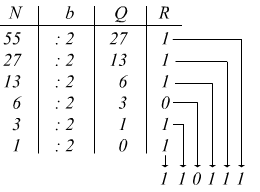

55,125(10) in base 10 = 110111,001(2) in base 2
Conversione di un numero da una base b1 ad una base b2
In generale è opportuno che il passaggio tra numeri di diverse basi venga eseguito utilizzando come base intermedia 10, cioè la conversione tra una base b1 e una base b2 può essere fatta secondo lo schema :
![]()
questo perchè non siamo in grado di calcolare rapidamente moltiplicazioni e divisioni in basi diverse dal 10. In informatica e nell'elettronica dei sistemi digitali le basi più frequenti sono 2, 8 e 16; possiamo vedere come le conversioni in questo caso siano quasi immediate
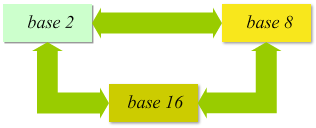
Conversione di un numero da base 2 a base 8
|
base 8
OCT |
base 2
BIN |
|
0
|
000
|
|
1
|
001
|
|
2
|
010
|
|
3
|
011
|
|
4
|
100
|
|
5
|
101
|
|
6
|
110
|
|
7
|
111
|
In questo caso, senza passare per la base intermedia 10, si scompone il numero binario in terzetti di cifre raggruppandole a partire dall'LSB (Least Significant Bit ≡ bit meno pesante) e applicando per ogni terzetto ottenuto, la conversione binario - ottale.
Verifichiamo la validità di questa tecnica convertendo 101011(2) in base 8
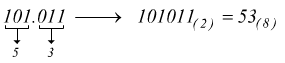
Come detto, il raggruppamento va eseguito partendo dall'LSB e, nel caso sia necessario, si possono aggiungere degli zeri davanti al MSB (Most Significant Bit ≡ bit più pesante) per formare il terzetto completo. Vediamo un altro esempio.
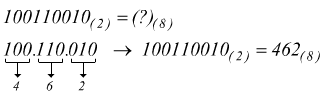
oppure
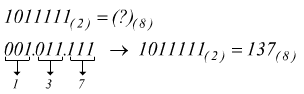
in quest'ultimo caso abbiamo dovuto aggiungere degli zeri davanti al MSB.
Con i decimali :
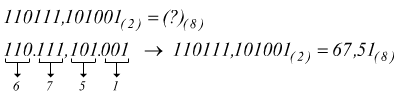
Conversione di un numero da base 8 a base 2
Anche la conversione da ottale a binario può essere eseguita immediatamente osservando la tabella precedente
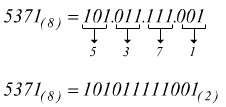
con i decimali
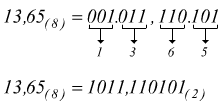
Conversione di un numero da base 2 a base 16
Anche in questo caso, senza passare dalla base intermedia 10, il numero binario da convertire viene scomposto in nibble (gruppi di 4 bit) raggruppate a partire dall'LSB applicando la tabella di conversione qui riportata.
|
base 16
HEX |
base 2
BIN |
|
0
|
0000
|
|
1
|
0001
|
|
2
|
0010
|
|
3
|
0011
|
|
4
|
0100
|
|
5
|
0101
|
|
6
|
0110
|
|
7
|
0111
|
|
8
|
1000
|
|
9
|
1001
|
|
A
|
1010
|
|
B
|
1011
|
|
C
|
1100
|
|
D
|
1101
|
|
E
|
1110
|
|
F
|
1111
|
esempio :
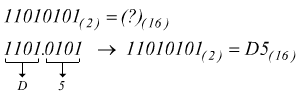
altro esempio:
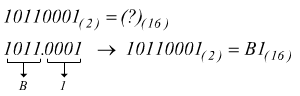
ulteriore esempio:
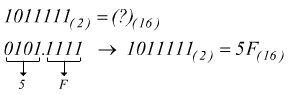
con i decimali
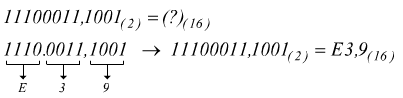
Conversione di un numero da base 8 a base 16 e viceversa
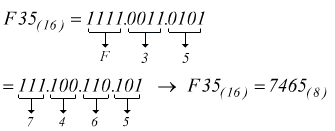
Per questo tipo di conversione si usano entrambe le tabelle OCT → BIN ed HEX → BIN passando attraverso la numerazione binaria, con l'impacchettamento opportuno di cifre (tre bit per l'ottale e quattro bit per l'esadecimale)
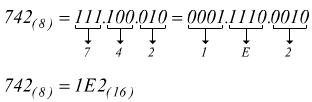
oppure
 edutecnica
edutecnica