Automi
Col termine automa si indica usualmente un apparato in grado di svolgere
un'attività senza l'intervento dell'uomo.
Con il termine apparato si sottintende un sistema che riceve dei comandi
(input) esterni e fornisce risposte o azioni in uscita (output).
Esempi di automi presenti nella vita quotidiana sono: l'ascensore, la lavatrice, un distributore automatico di merendine, il semaforo, etc.. Ad esempio, il semaforo è un dispositivo che accende una luce di colore diverso ogni volta che, allo scadere di un tempo prefissato, arriva un segnale di sincronismo e il semaforo può accendere e spegnere una delle luci gialla rossa e verde. Lo schema di flusso di un semaforo è indicato nel disegno seguente
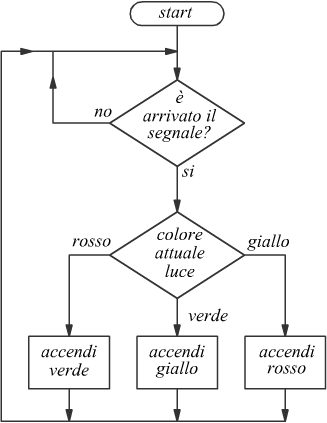
Per indicare il funzionamento degli automi si usano degli schemi chiamati grafi. Il grafo rappresentativo di un semaforo è il seguente:
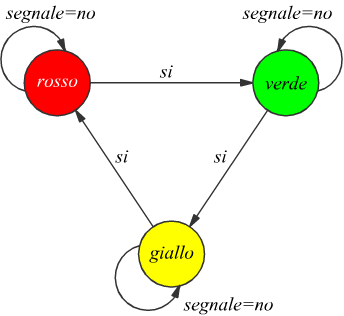
I grafi sono costituiti da nodi (cerchi) e da archi orientati (linee dotate di freccia che uniscono i nodi). I nodi rappresentano le condizioni logiche (dove si prendono le decisioni) che sottendono il funzionamento dell'automa, nella situazione in cui arriva un certo ingresso. Gli archi orientati indicano un evento completo e specificano anche il valore di ingresso ed il valore dell'uscita che provoca la transizione. Questi valori sono di solito riportati sopra l'arco e sono separati da una virgola. Nei grafi, talvolta viene usato il simbolo
![]()
per indicare in quale condizione l'automa passa quando viene fornita l'energia di alimentazione al dispositivo. Un altro sistema molto semplice è il cancello motorizzato che può essere assimilato al funzionamento di un interruttore per lampadina. Se indichiamo con push il fatto di aver premuto il pulsante di comando e con C (Chiuso) ed A(aperto) si avrebbero soltanto due stati indicati nel seguente grafo.
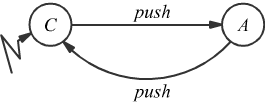
Con le nostre conoscenze di elettronica digitale possiamo facilmente pilotare il funzionamento del cancello con un semplice latch SR
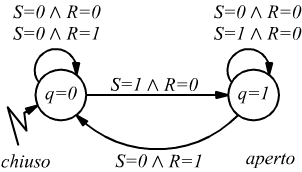
Dove con l'identificatore "q" abbiamo indicato lo stato dell'automa: q=0=chiuso,
q=1=aperto.
Questo appena descritto può già essere definito un automa a stati finiti
o macchina a stati finiti (FSM = Finite State Machine). I nodi (come nel
caso del semaforo) sono rappresentativi degli stati. Gli archi sono delle
transizioni di stato causate da eventi esterni (input). Le uscite possono
essere associate sia agli stati che alle transizioni.
In teoria si potrebbe far funzionare il cancello anche in quest'ultimoo modo, ma sappiamo che alcune precauzioni vanno prese, ad esempio se durante la fase di chiusura la fotocellula segnala la presenza di un ingombro sulla linea del binario, il cancello si deve immediatamente riaprire e poi non sarebbe prudente attivare il comando di chiusura quando il cancello si sta aprendo. Decidiamo, allora, di modificare il nostro schema tenendo conto delle seguenti variabili di ingresso e di uscita
INGRESSI
A = comando di apertura
C = comando di chiusura
USCITE
M = motore on/off (1= on, 0=off)
S = senso di rotazione del motore (1=apre 0=chiude)
sappiamo, infatti, che per chiudere il motore deve girare in senso contrario
rispetto all'apertura.
Supponendo che i comandi di input siano mutuamente
esclusivi (cioè in ogni istante al più uno di loro può essere vero),
avremo allora il seguente schema
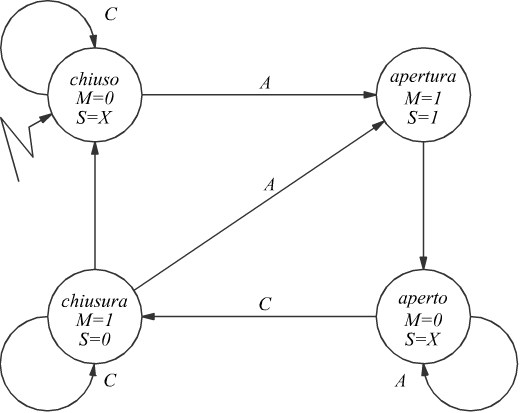
In questa FSM, abbiamo usato simboli facilmente comprensibili.
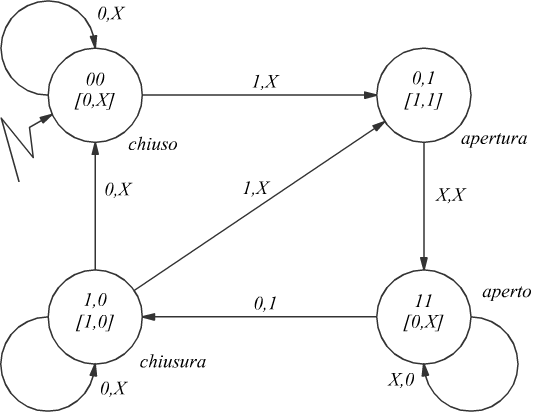
Adesso passiamo alla notazione binaria. Adottiamo alcune convenzioni (arbitrarie):
gli ingressi siano ordinati in questo modo: A,C, quindi 10 indica A=1, C=0.
L'ordine delle uscite sia M, S.
Numeriamo poi gli stati
Chiuso = 00
In apertura =01
Aperto = 11
In chiusura = 10
Si vede come durante la fase di chiusura sia possibile riattivare l'apertura;
questo in pratica avviene in base ad una fotocellula, che in caso venga
rilevato un ingombro sul binario di chiusura riavvia automaticamente la
procedura di apertura.
Associamo le uscite ad ogni stato, questo perché in questo esempio le uscite
non dipendono dagli input (ma solo dallo stato, altrimenti, le uscite sarebbero
associate alle transizioni fra stati) . Se indichiamo X uno stato di indifferenza
(0/1)
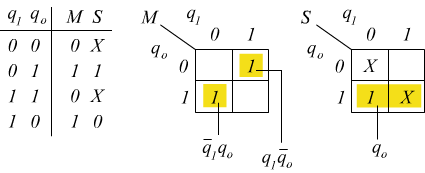
La relazione tra gli stati e le uscite sarà M=q1qo+q1qo
in pratica ![]() (EX-OR)
mentre è S=qo .
(EX-OR)
mentre è S=qo .
Trascriviamo la dipendenza dello stato successivo da stati e input in
una tabella della verità, indichiamo:
qo, q1 = stato corrente
qo', q1' = stato successivo
Guardando il diagramma dell'Automa a Stati finiti, per ogni stato corrente,
e per ogni input, segniamo la codifica dello stato successivo (nelle due
colonne di output)

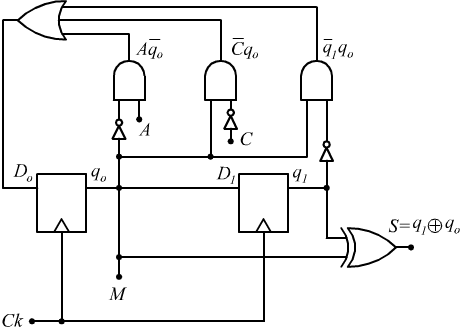
per memorizzare gli stati useremo dei flip-flop D.
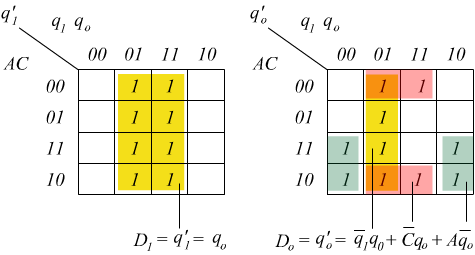
otteniamo dunque il seguente circuito:
Modelli di riferimento per gli automi
Dall'esterno un automa si presenta come una rete combinatoria (porte AND OR e NOT collegate assieme) ad h ingressi e w uscite; è come se l'automa fosse privo di memoria anche se le uscite ad ogni istante dipendono sia dagli ingressi attuali sia dalla storia degli ingressi precedenti. Ingressi uguali possono produrre uscite diverse se diverse sono le condizioni iniziali.

Il modello matematico di automa è rappresentato da un sistema di equazioni del tipo
z1=f(x1 , x2 , .., xh, t)
z2=f(x1 , x2 , .., xh, t)
. . .
zw=f(x1 , x2 , .., xh, t)
Per definizione un automa funziona correttamente se è in grado di ricordare in una memoria le informazioni relative agli ingressi precedenti:chiamiamo stato dell'automa, in un certo istante t, la configurazione della memoria in quell'istante.
Come abbiamo visto nell'esempio,per ricordare in quale stato si trova l'automa quando si presenta ai suoi ingressi una nuova configurazione, è sufficiente associare una particolare configurazione ad ogni stato diverso. Il numero degli stati dell'automa è considerato finito. Due configurazioni di ingresso uguali possono produrre configurazioni delle uscite diverse, se diverso è lo stato in cui si trova l'automa.
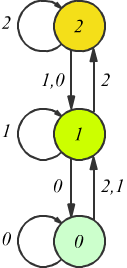
Per esempio, nell'automa
ascensore, se viene premuto il bottone relativo al primo piano, l'ascensore
in funzione anche del piano in cui si trova, può salire, scendere o restare
fermo. Con questa sostituzione le uscite dipendono dagli ingressi e dallo
stato dell'automa. Lo stato conserva gli effetti delle configurazioni degli
ingressi precedenti sotto forma di segnali interni.
L'automa ascensore disegnato, ha tre stati distinti (piano terra, primo
piano e secondo piano): per identificare univocamente ogni stato bastano
2 segnali interni (bit). In generale, se l'insieme degli stati Q di un automa
è finito, indicando con |Q| la sua cardinalità (numero degli stati), possiamo
codificare univocamente gli stati con un numero k di variabili binarie (variabili
di stato), dato dalle seguenti relazioni: 2k-1 <|Q| 2k .
Nell'esempio dell'ascensore |Q| = 3 e quindi k vale 2.
Lo stato quindi è rappresentato attraverso la configurazione di k variabili
interne (endogene) y1,y2,…,yk.
Le w uscite sono funzioni delle h variabili esterne (esogene) e delle
k variabili interne. La relazione precedente può essere scritta nel seguente
modo:
zj = f(x1,x2,…xh,y1,y2,…yk)
con j = 1,2,... w .
Si supponga che il comportamento dell'automa sia deterministico, cioè il nuovo stato raggiunto sia univocamente determinato dallo stato attuale e dagli ingressi. Indicando yn ed yn+1, rispettivamente il valore delle variabili interne in un certo istante (stato attuale) e all'istante successivo (stato futuro) si può scrivere il modello matematico per gli automi come:
zj=f(x1, x2,.. xn,y1n,
y2n,.. ykn) con j=1,2,..w
yin+1=g(x1, x2,.. xn,y1n,
y2n,.. ykn) con i=1,2,..k
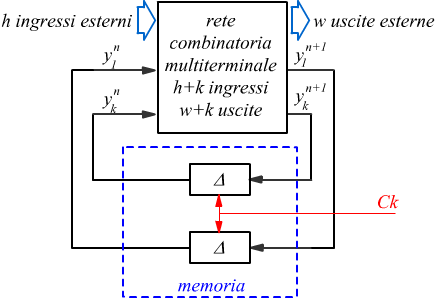
Lo schema disegnato prima, sintetizza le equazioni precedenti di un circuito combinatorio multiterminale ad h+k ingressi e ad w+k uscite. In questo caso il termine "multiterminale" indica un circuito con più ingressi e più uscite.
Il disegno, mette in evidenza che tra le uscite interne e gli ingressi
interni non vi è alcun legame.
Da quanto detto in precedenza, si può dire che le uscite interne non sono
altro che gli ingressi interni, per la successiva configurazione degli ingressi
esterni.
Per esempio, quando l'ascensore si trova al piano terra (stato attuale)
e si seleziona il bottone 2, l'ascensore sale per raggiungere il secondo
piano (stato futuro); se successivamente sisi seleziona un altro bottone,
lo stato di partenza diventa il secondo piano e non il piano terra. In pratica,
il piano raggiunto, diventa il piano di partenza per l'ingresso successivo.
Per legare le variabili yn+1 ed yn basta usare un
dispositivo di ritardo Δ, definito come elemento ad un solo ingresso
e ad una sola uscitacon la funzione di riportare l'ingresso in uscita con
un certo ritardo yn+1(t+Δ)=yn .
![]()
Con questi nuovi elementi si può rappresentare un automa come l'interconnessione
di una rete combinatoria e di una rete di memoria.
La rete combinatoria descrive il comportamento esterno e la rete di memoria
descrive il suo comportamento interno.
Il generatore di clock è un generatore di segnali periodici che permette
la sincronizzazione delle uscite con gli ingressi.
Lo stato del sistema in un certo istante è rappresentato dai valori delle
variabili di stato, occorre pertanto che questi valori siano presenti simultaneamente.
Automi a stati finiti
L'automa è un sistema dinamico discreto, invariante e a stati finiti,
caratterizzato da h ingressi e w uscite definito da:
● un insieme finito di valori di ingresso
I
● un insieme finito di valori di uscita U
● un insieme finito degli stati Q
● un insieme di regole definite da una funzione
di stato τ che specifica lo stato futuro noto lo stato attuale e l'ingresso
τ : Q·I→Q
● un insieme di regole definite da una funzione
di trasformazione delle uscite ω che fornisce il valore d'uscita noti
lo stato attuale e l'ingresso attuale , ω : Q·I→U
Un automa si dice proprio quando la sua uscita non dipende istantaneamente dall'ingresso, si dice improprio quando la sua uscita dipende istantaneamente dall'ingresso.
Lo schema seguente rappresenta l'automa di Mealy, nel quale l'uscita dipende direttamente ed istantaneamente dall'ingresso; esso è infatti un automa improprio.
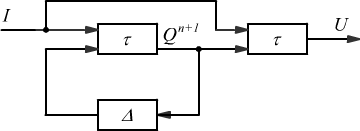
Lo schema seguente rappresenta l'automa di Moore, nel quale l'uscita non dipende dall'ingresso; esso è infatti un automa proprio.
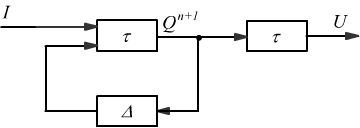
I due modelli sono considerati equivalenti; da un automa di Mealy si può ottenere un automa di Moore e viceversa, l'automa di Mealy risulta essere, in genere, più rapido.
 edutecnica
edutecnica