Resistenza dei materiali
In Fisica si definiscono i solidi
come corpi che mantengono una forma ed un volume proprio.
Questa definizione non è molto esatta perchè notiamo che quando ad un
solido si applicano forze esterne la forma tende a modificarsi a secondo
dell'intensità delle forze.
Se le forze esterne, applicate ad un corpo si mantengono entro dei limiti
moderati il corpo si deforma solo momentaneamente e poi tende a riprendere
la forma primitiva al cessare delle forze applicate.
Si ha in questo caso una deformazione elastica.
Se si applicano forze di grande intensità la deformazione subita dal
corpo potrà risultare permanente e si avrà in questo caso una deformazione
plastica.
E' chiaro che nel settore delle costruzioni le forze applicate devono
essere entro limiti tali da provocare solo deformazioni elastiche, cioè
non devono superare il limite di elasticità del materiale impiegato.
Entro questo limite non solo le deformazioni sono elastiche ma sono
proporzionali alle forze applicate, cioè, raddoppiando le forze raddoppiano
anche le deformazioni. Come indicato nella legge di Hooke (1678)
![]()
La resistenza dei materiali è lo studio connesso alle proprietà di rigidità, elasticità e resistenza degli elementi strutturali da costruzione.
Ipotizziamo un corpo solido, sul quale agiscano delle forze esterne; per effetto delle forze esterne si sviluppano all'interno del corpo forze elementari chiamate tensioni interne proporzionali all'intensità delle forze esterne. Queste forze tendono a deformare il corpo solido considerato.
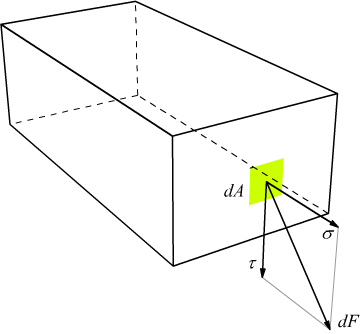
Consideriamo un corpo di sezione trasversale A ed una area elementare dA (infinitesima) della sezione sulla quale agisce una forza elementare dF; definiamo la tensione t ( di fatto una pressione) come
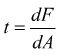 [N/mm2]
[N/mm2]
La tensione differenziale t viene decomposta lungo la normale all'area
elementare dA e lungo una generica direzione giacente sul piano dA originando
le due componenti
•la tensione normale σ
• la tensione tangente τ
Prova di trazione
La prova di trazione è un metodo che consente di determinare il carico unitario di rottura e di snervamento.
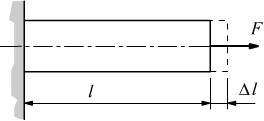
Per eseguire la prova si utilizzano delle provette definite dalla norma UNI-556. Durante il test la provetta viene assoggettata ad una forza assiale crescente e la macchina che esegue la prova è in grado di tracciare su un diagramma carichi-allungamenti dove si possono individuare le seguenti zone:
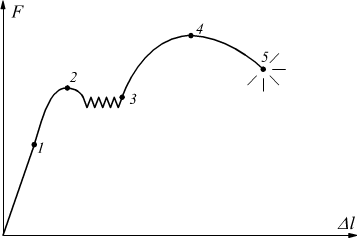
a) Campo elastico (0-1) è la zona in cui gli allungamenti Δl sono proporzionali ai carichi applicati F secondo la legge di Hooke
![]() con
con
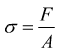 carico
unitario [N/mm2]
carico
unitario [N/mm2]
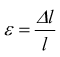 allungamento
relativo [adimensionale]
allungamento
relativo [adimensionale]
E=modulo di elasticità (di Young); per gli acciai E=200.000÷210.000
N/mm2.
Osserviamo che (l) ed (A) sono delle costanti, quindi σ è proporzionale
ad F ed ε proporzionale a Δl .
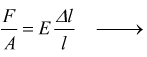
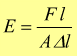
Quest'ultima formulazione della legge di Hooke è quella che viene usata normalmente per calcolare gli allungamenti nelle sollecitazioni a trazione.
A Fino al punto 1 la provetta non subisce deformazioni permanenti, cioè, se si toglie dalla provetta il carico, essa perde l'allungamento Δl e torna alla lunghezza iniziale l.
Aumentando ulteriormente il carico si passa nella zona (1-2) chiamata campo di plasticità; in questo tratto non è più valida la legge di Hooke e se la provetta viene scaricata, essa non torna più alla lunghezza originaria l ma subisce un allungamento finale permanente Δl.
B Snervamento: è il tratto (2-3) caratterizzato da un notevole allungamento della provetta , senza che F aumenti in modo considerevole.
C Incrudimento: zona (3-4) dove viene applicato il carico massimo Fmax e la provetta si assottiglia deformandosi, qui il materiale diventa inutilizzabile per scopi costruttivi.
D Rottura: il tratto (4-5) alla fine del quale si ha la rottura della provetta per un carico FR<Fmax perché a parità di volume del materiale a causa dell'allungamento si ha una diminuzione della sezione della provetta.
Definiamo 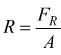 carico
unitario di rottura [N/mm2]
carico
unitario di rottura [N/mm2]
Criteri di resistenza
Una volta noto il carico unitario di rottura di un dato materiale è possibile definire
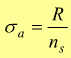 carico
unitario di sicurezza [N/mm2] (#)
carico
unitario di sicurezza [N/mm2] (#)
che è la massima tensione ammissibile per mantenere l'elemento meccanico
considerato in condizioni di sicurezza, cioè in modo che esso resista
alle varie sollecitazioni senza deformarsi.
Si adotta come grado di sicurezza ns
ns=3÷5 per gli acciai
ns=7÷9 per le ghise
ns=8÷10 per il legno
Il grado di sicurezza deve essere scelto arbitrariamente dal progettista. Quando un elemento è sottoposto a forze esterne, al suo interno, si instaurano delle tensioni σ assiale e τ tangenziale. Bisogna sempre assicurarsi che
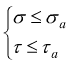
Queste considerazioni valgono solo nel caso di carichi
statici, cioè, nel caso di sollecitazioni applicate in modo graduale,
senza urto e persistenti nel tempo. Se invece i carichi sono variabili
nel tempo, si parla di carichi dinamici.
Carichi dinamici
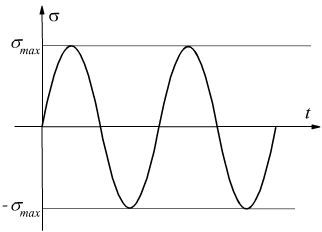
Se il carico varia ciclicamente da un valore massimo ad un valore minimo, si applica il criterio
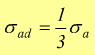
gli sforzi che si instaurano non devono superare il valore di σad così ottenuto. Per gli acciai si conclude che se siamo in condizioni dinamiche, il carico di sicurezza può essere ottenuto dividendo il carico di rottura da un minimo di 9 ad un massimo di 15.
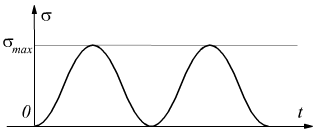
Il carico dinamico potrebbe anche essere di tipo 'pulsante' cioè variare da un valore massimo ad un valore nullo. In tal caso si ha
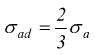
Equazione di stabilità per la trazione
In base a quando si è potuto constatare, si ha una sollecitazione di trazione quando su una trave agisce una forza F lungo un suo asse e si verifica un allungamento Δl.
Se ci riferiamo al disegno iniziale vediamo che gli sforzi che tenderanno ad allungare il corpo sono le componenti σ della sollecitazione (normali alla superficie) tutti questi sforzi elementari andranno sommati e considerati globalmente andando a definire la condizione di equilibrio
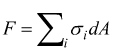 ipotizzando
tutti i σi costanti nella stessa direzione
ipotizzando
tutti i σi costanti nella stessa direzione 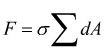
ma la somma delle aree elementari va a costituire la superficie della sezione trasversale alla direzione dello sforzo
![]()
Per valutare la resistenza alla trazione di un dato materiale basterà conoscere preventivamente il σa (ammissibile) con l'equazione (#) e verificare che sia
![]()
se la precedente relazione è verificata allora il materiale sta 'operando' in condizioni di sicurezza.
Di seguito viene riportata una tabella contenente valori orientativi sul carico unitario di rottura dei principali acciai da costruzione in base UNI EN 10025, dove con 'dimensione', si intende il diametro nel caso di una sezione circolare oppure la dimensione minima trasversale negli altri casi.
| Acciaio | Dimensione [mm] | R N/mm2 |
| Fe360 | 360 | |
| Fe490 | 490 | |
| Fe590 | 590 | |
| Fe690 | 690 | |
| C25 normalizzato |
Da 16 a 100 | 410 |
| C25 bonificato |
Fino a 16 Oltre 16 fino a 40 |
540 490 |
| C25 bonificato |
Fino a 16 Oltre 16 fino a 40 Oltre 40 fino a 100 Oltre 100 fino a 250 |
560 540 530 510 |
| C35 normalizzato |
Da 16 a 100 | 490 |
| C35 bonificato |
Fino a 16 Oltre 16 fino 40 Oltre 40 fino a 100 |
670 610 570 |
| C35 bonificato |
Fino a 16 Oltre 16 fino 40 Oltre 40 fino a 100 Oltre 100 fino a 250 |
560 550 540 520 |
| C40 normalizzato |
Da 16 a 100 | 570 |
| C40 bonificato |
Fino a 16 Oltre 16 fino a 40 Oltre 40 fino a 100 |
700 640 590 |
| C45 normalizzato |
Da 16 a 100 | 590 |
| C45 bonificato |
Fino a 16 Oltre 16 fino a 40 Oltre 40 fino a 100 |
730 690 640 |
| C60 bonificato |
Fino a 16 Oltre 16 fino a 40 Oltre 40 fino a 100 |
830 780 740 |
| 35 CrMo4 bonificato |
Fino a 16 Oltre 16 fino a 40 Oltre 40 fino a 100 Oltre 100 fino a 250 |
980 880 785 685 |
| 42 CrMo4 bonificato |
Fino a 16 Oltre 16 fino a 40 Oltre 40 fino a 100 Oltre 100 fino a 250 |
1080 980 880 735 |
| 39 NiCrMo3 bonificato | Fino a 16 Oltre 16 fino a 40 Oltre 40 fino a 100 Oltre 100 fino a 250 |
1030 980 880 685 |
| 30 NiCrMo 12 bonificato | Fino a 40 Oltre 40 fino a 100 Oltre 100 fino a 250 |
1225 1130 980 |
 edutecnica
edutecnica