Composizione di movimenti
Il moto rettilineo è un moto che si svolge in un'unica direzione e quindi in un'unica dimensione ma il moto di un corpo può essere assoggettato in due o tre dimensioni. Nel caso, ad esempio di un aereo in fase di decollo, osserviamo che il suo moto è la risultante di due spinte: quello dei motori in senso orizzontale e quello della spinta dell'aria sulle ali in senso verticale.
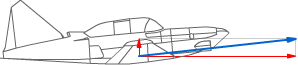
Un altro esempio è il moto di un proiettile sparato da un cannone con inclinazione
data. In tal caso, il corpo mobile, sarà soggetto ad una spinta sia orizzontale
che verticale, con l'ulteriore condizione che tale corpo, in senso verticale,
è soggetto anche ad un moto uniformemente accelerato dato dalla forza di
gravità con accelerazione g.
Si tratta, infatti, dello stesso fenomeno a cui può essere soggetto un pallone
di calcio o di basket durante il suo utilizzo convenzionale.
Posizione e spostamento
Il modo più semplice per individuare la posizione
di un punto materiale in uno spazio tridimensionale
è quella di usare il vettore posizione r⃗:
![]()
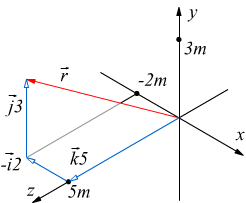
dove i⃗,
j⃗
e k⃗
sono i versori degli assi coordinati rispettivamente x, y e z. Ricordiamo
che un versore è un vettore di modulo unitario che ha la stessa direzione
e verso dell'asse a cui è associato. Le quantità x, y e z sono le tre componenti
scalari di tale vettore. Per esempio utilizzando delle misure in metri,
![]()
con coordinate (-2 m, 3 m, 5 m). Lungo l'asse x la particella è a -2 m dall'origine,
nella direzione lungo l'asse y si trova a 3 m dall'origine, lungo l'asse
z si trova a 5 m dall'origine, nella direzione.
Quando una particella si muove, il suo vettore posizione cambia in che il vettore r⃗ si estenda sempre alla particella dal punto di riferimento (l'origine). Se la posizione della particella cambia durante un certo intervallo di tempo Δt, il vettore posizione cambia, diciamo , da r⃗1 a r⃗2, quindi chiamiamo Δr⃗ lo spostamento delle particelle durante tale intervallo di tempo è
![]()
usando la notazione vettoriale avremo
![]()
che si può scrivere nella forma
![]()
dove le coordinate (x1, y1, z1) corrispondono
al vettore di posizione r⃗1
e alle coordinate (x2, y2, z2) corrispondono
al vettore di posizione r⃗2
. Possiamo anche riscrivere lo spostamento sostituendo Δx per (x2
x1), Δy per (y2 y1) e Δz per
(z2 z1):
![]()
Velocità
Se una particella si sposta da un punto a un altro, potremmo aver bisogno
di sapere quanto velocemente essa si sposta. Come nel caso del moto rettilineo
possiamo definire le due quantità : velocità
media e velocità istantanea. Tuttavia,
qui dobbiamo considerare queste quantità come vettori e usare una notazione
vettoriale.
Se una particella si muove attraverso uno spostamento Δr⃗
in un intervallo di tempo Δt, allora la sua la velocità
media v⃗m
è definita come
![]() che
può essere riscritta come
che
può essere riscritta come
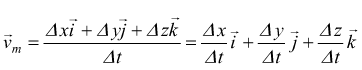
ad esempio se una particella effettua uno spostamento 15i⃗+6k⃗ [m] in un intervallo Δt=3 s
![]()
Quando parliamo della velocità di una particella, di solito intendiamo la velocità istantanea. Questo è il valore a cui si avvicina v⃗m mentre riduciamo l'intervallo di tempo Δt a 0. Usando l'analisi matematica di calcolo, possiamo scrivere come derivata
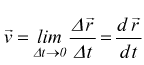
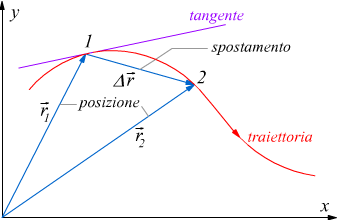
Nel disegno si vede il percorso di una particella limitata al piano xy.
Durante l'intervallo di tempo Δt, il vettore di posizione cambia da
r⃗1
a r⃗2
e il lo spostamento delle particelle è Δr⃗.
Per trovare la velocità istantanea della particella, diciamo, istante t1
(quando il la particella è nella posizione 1), riduciamo l'intervallo Δt
a 0. Mentre lo facciamo, il vettore r⃗2
si sposta verso r⃗1
e Δr⃗
si restringe. La direzione di Δr⃗/Δt=v⃗m
è data dalla direzione di Δr⃗
.
Possiamo quindi dire che la direzione della velocità media v⃗m
si avvicina a direzione della linea tangente al percorso della particella
in posizione 1. Assieme alla direzione, anche l'intensità della velocità
media v⃗m
si avvicina all'intensità della velocità istantanea:
v⃗
al tempo t1.
Al limite, Δt; → 0 abbiamo v⃗m → v⃗ e, soprattutto, qui, v⃗m assume la direzione della retta tangente alla traiettoria nel punto 1, quindi: v⃗ ha anch'essa quella direzione:
La direzione della velocità istantanea di una particella è sempre tangente alla percorso della particella nella posizione della particella.
Si puòscrivere l'eq. precedente in forma vettoriale 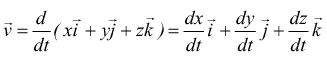 scrivendo
così
scrivendo
così
![]() con
i componenti scalari
con
i componenti scalari 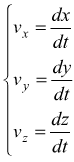
Cioè, dx/dt è il componente scalare di v⃗ lungo l'asse x, quindi possiamo trovare i componenti scalari di v⃗ differenziando i componenti scalari di r⃗.
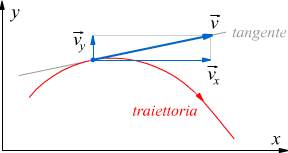
Nel disegno, si mostra un vettore di velocità v⃗ e i suoi componenti scalari x ed y. Nota che v⃗ è tangente al percorso della particella nella posizione della particella; esso rappresenta la direzione di marcia istantanea della particella che si trova sempre alla coda del vettore, e la sua lunghezza, che rappresenta l'intensità della velocità.
Accelerazione
Quando la velocità di una particella cambia da v⃗1 a v⃗2 in un intervallo di tempo Δt, è la sua accelerazione media a⃗m durante Δt viene definita come
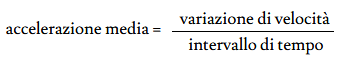 ; facendo
tendere Δt → 0 otteniamo la velocità istantanea
; facendo
tendere Δt → 0 otteniamo la velocità istantanea
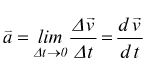
se la velocità cambia intensità oppure direzione
(o entrambi) la particella deve avere una accelerazione.
Rispetto alle componenti scalari avremo
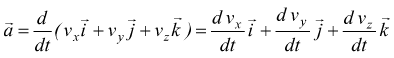 che può essere riscritta come
che può essere riscritta come
![]() con
con 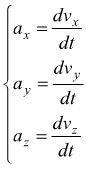
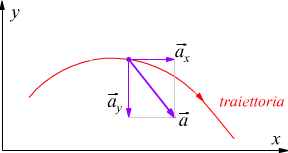
come nel caso della velocità il vettore accelerazione ha la coda del vettore
collocato sul punto materiale in movimento.
Nel moto curvilineo la velocità cambia, in generale, sia in modulo (intensità)
che in direzione. Il modulo della velocità varia in quanto si possono verificare
sia delle accelerazioni che dei rallentamenti. La direzione della velocità
cambia in quanto essa è tangente alla traiettoria e la traiettoria si incurva
continuamente.
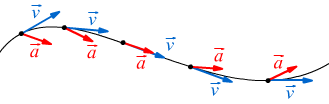
L'accelerazione è un vettore che ha la stessa direzione della variazione istantanea della velocità. Poiché la velocità cambia nella direzione in cui la traiettoria si incurva, l'accelerazione è sempre diretta verso la concavità della curva ed in generale non è ne tangente ne perpendicolare alla traiettoria. come si vede nel disegno riportato sopra.
Moto di proiettili
Come si è detto moto di un proiettile sparato da un cannone con inclinazione data è un tipico esempio di moto curvilineo bidimensionale. In tal caso, il corpo mobile, sarà soggetto ad una spinta sia orizzontale che verticale, con l'ulteriore condizione che tale corpo, in senso verticale, è soggetto anche ad un moto uniformemente accelerato dato dalla forza di gravità con accelerazione g.
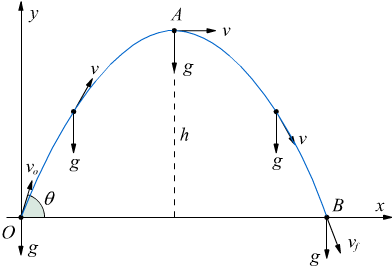
Supponendo di conoscere la velocità iniziale vo e l'angolo di inclinazione θ:
![]() con
con
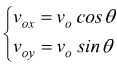
In questo tipo di moto la componente della velocità in orizzontale è un moto uniforme, mentre la componente verticale è un moto uniformemente accelerato influenzato dalla gravità g. Per tale componente useremo l'equazione che regola la velocità per il moto uniformemente accelerato:
![]() ovviamente
poniamo to=0, mentre l'accelerazione a= - g.
ovviamente
poniamo to=0, mentre l'accelerazione a= - g.
Quando il proiettile arriva in A : voy=0 dato che voy=gt
sarà passato un tempo t dato da 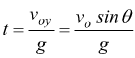
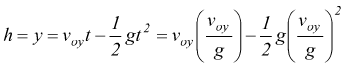
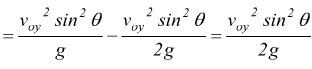
Il tempo necessario affinché il proiettile arrivi in B si ottiene ponendo y=0 nella
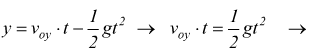
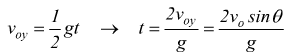
La gittata OB si ottiene inserendo tale tempo nella
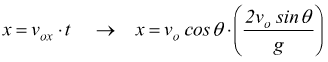
La gittata massima si ottiene per θ=45° derivando ed uguagliando a 0 l'equazione precedente. L'equazione della traiettoria si ottiene eliminando t dal sistema precedente:
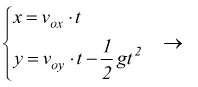
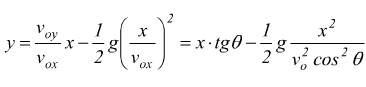
45°
35 m/s
0 s
vox=24.74 m/s
voy=24.74 m/s
hmax=31.21 m
gittata=124.87 m
x=0 y=0 m
 edutecnica
edutecnica