Ruote dentate coniche a denti diritti
Questo tipo di ruote dentate è usato per trasmettere potenza, con moto rotatorio, fra alberi concorrenti, cioè, alberi ( non paralleli ) che hanno gli assi passanti per uno stesso punto.
Tutti gli elementi costruttivi di una coppia di ruote dentate coniche, dipendono dagli angoli di semi apertura δ1 e δ2 dei coni primitivi delle due ruote.
Per costruire una coppia di ruote dentate coniche, bisogna conoscere,
prima di tutto, l'angolo ζ fra gli assi delle ruote e dei
numeri dei giri n1 ed n2 delle ruote motrice e
condotta.
Poniamo per fare un esempio n1
= 300g/m n2 = 450g/m;
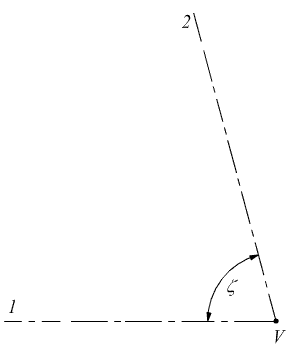
ζ= 75° .
Si tracciano l'asse 1 dall'albero motore all'asse 2 dell'albero condotto, formati fra loro l'angolo di 75° e concorrenti nel punto V.
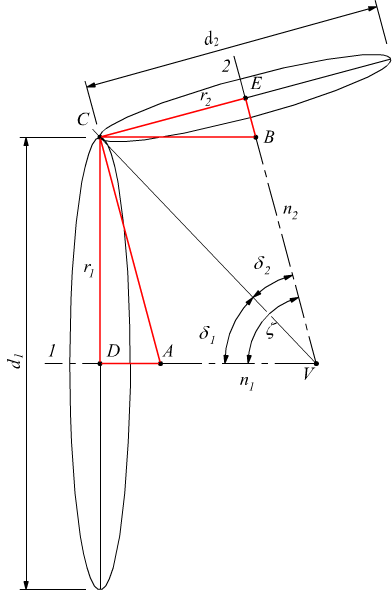
Da questo punto si riporta sull'asse 1 un segmento VA proporzionale
ad n1 (ad es. ipotizzando un fattore di scala pari a 1/2
VA=150mm ~ 300g/m) e sull'asse 2 un segmento VB proporzionale ad n2
( ad es. VB=225mm ~ 450g/m) .
Poi si costruisce il parallelogramma su questi due segmenti. La diagonale VC del parallelogramma VACB rappresentata la generatrice di contatto dei coni primitivi delle due ruote. Il cono primitivo della motrice ha raggio base r1 e diametro primitivo d1 = 2·r1.
Il cono primitivo della condotta ha raggio base r2 e diametro primitivo d2 = 2· r2 . I triangoli ACD e BCE sono simili, perché hanno tutti gli angoli uguali; quindi i loro lati omologhi sono proporzionali.
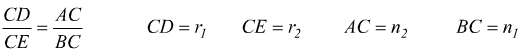
 i=rapporto
di trasmissione
i=rapporto
di trasmissione
In questo caso risulta:
L'angolo di semiapertura del cono primitivo 1 : δ1 =
45°.
L'angolo di semiapertura del cono primitivo 2: δ2
= 30° .
In pratica, invece di considerare i coni primitivi indefiniti, si considerano
i corrispondenti tronchi di cono, di una certa altezza, limitati esternamente
da coni complementari, i cui vertici V1 e V2 si
ottengono conducendo dal punto C la perpendicolare alla generatrice
VC.
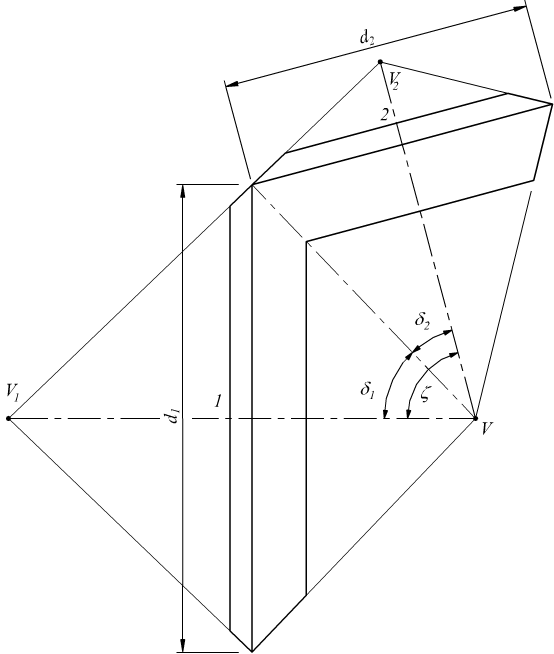
Sui tronchi di cono primitivi si costruiscono poi i denti z1 e z2 della motrice e della condotta e si ottiene una coppia di ruote dentate coniche, con rapporto:
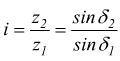 infatti
si nota
infatti
si nota 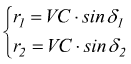 se si usano i due raggi primitivi si nota che:
se si usano i due raggi primitivi si nota che:
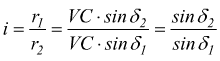 si
ottiene il sistema
si
ottiene il sistema
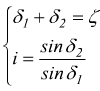 che
permette di trovare δ1 e δ2.
che
permette di trovare δ1 e δ2.
Nel caso particolare in
cui 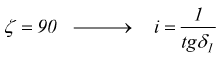
Elementi di una ruota dentata conica
Nella figura seguente viene rappresenta la sezione una ruota dentata conica con i suoi elementi caratteristici.
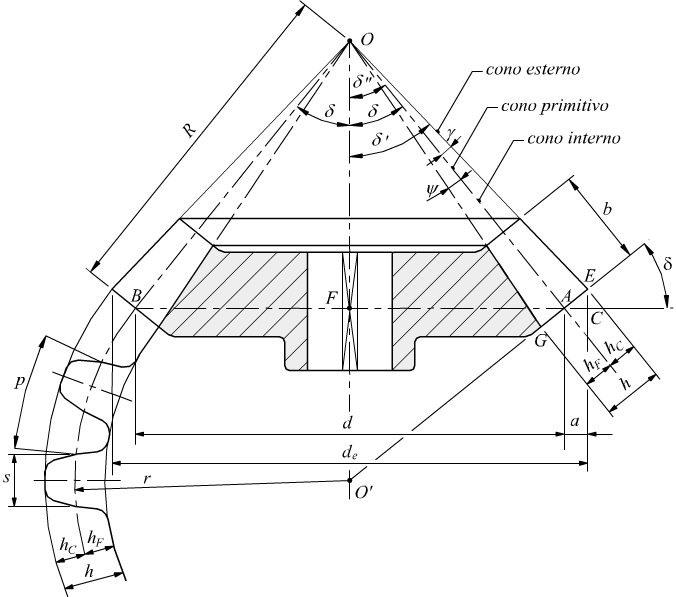
m= modulo della dentatura;
z= numero dei denti;
δ= angolo di semiapertura del cono primitivo
δ'=angolo di semiconicità esterna
δ"=angolo di semiconicità interna
hC=addendum
hF=dedendum
h=altezza del dente
b=larghezza del dente
γ=angolo dell'addendum
ψ=angolo del dedendum
d=diametro primitivo
de=diametro di testa ( diametro esterno )
R=lunghezza del raggio del cono primitivo
p=passo della dentatura
r=raggio primitivo del cono complementare
Fissato il modulo, le formule per il dimensionamento sono analoghe a quelle delle ruote cilindriche a denti diritti.
![]() diametro
primitivo
diametro
primitivo
![]() passo
passo
![]() addendum
addendum
![]() dedendum
dedendum
![]() altezza del dente
altezza del dente
![]() diametro
di testa ( diametro esterno )
diametro
di testa ( diametro esterno )
![]() larghezza
della fascia dentata
larghezza
della fascia dentata
( per evitare problemi di ingranamento si raccomanda b=8·m ). Poi si ricava
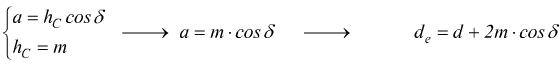
Dal triangolo rettangolo BOF si ottiene poi
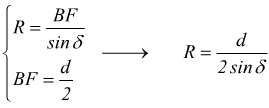 lunghezza
del raggio del cono primitivo
lunghezza
del raggio del cono primitivo
In modo analogo dal triangolo BO'F si ricava
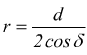 raggio
primitivo del cono complementare
raggio
primitivo del cono complementare
Sempre dal disegno si ricava l'angolo dell'addendum:
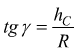
Mentre l'angolo del dedendum è: 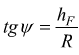
Il profilo dei denti di una ruota conica si può disegnare come se si trattasse di una dentatura cilindrica di raggio primitivo r con un numero di denti fittizio (ideale) zi esprimibile come
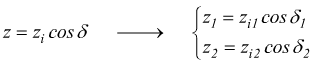
con z=numero dei denti della ruota conica. Questo comporta che possiamo usare la seguente formula valida per le ruote cilindriche (che qui riteniamo ideali):
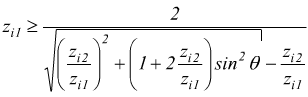
che fornisce il minimo numero di denti per la ruota motrice nel caso
di profili cilindrici
( quasi sempre θ=20°) . Se conosciamo il rapporto di trasmissione
fra le ruote coniche si può scrivere:
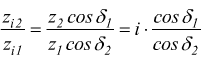 avendo
questo rapporto si calcola in questo modo zi1 minimo
avendo
questo rapporto si calcola in questo modo zi1 minimo
![]()
Si ottiene così, il numero minimo dei denti della ruota motrice
conica.
Poi col rapporto di trasmissione si calcola il numero dei denti della
ruota mossa.
Dimensionamento di una ruota dentata conica
Il dimensionamento a flessione dei denti può essere fatto con le stesse formule usate nel caso delle ruote cilindriche, ma le ruote coniche sono rastremate e quindi le formule, possono solo far riferimento ad un modulo medio.
Se conosciamo la potenza trasmessa e σT= carico
di sicurezza unitario dinamico ( σamd )
la coppia MT si ottiene come
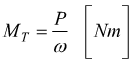 oppure
oppure
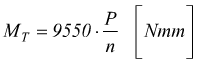
così si trova il modulo medio:
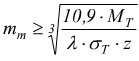 se
&lambda≈10
se
&lambda≈10 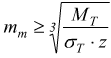
oppure bisogna conoscere la forza e la velocità periferica ; da quest'ultima si può ricavare, tramite le tabelle, il carico di sicurezza (in funzione della velocità). E' possibile eseguire il calcolo conoscendo solo potenza trasmessa e velocità periferica
 poi
per il calcolo del modulo medio si applica la seguente:
poi
per il calcolo del modulo medio si applica la seguente:
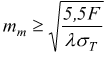 se
&lambda≈10
se
&lambda≈10 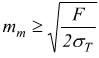
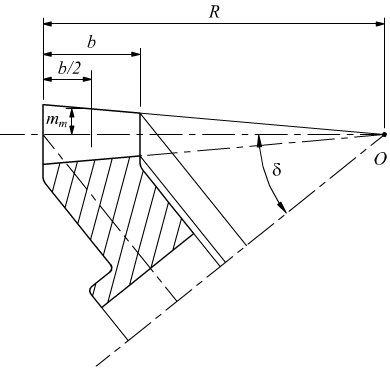
Calcolato il modulo medio si ottiene il modulo nominale. Osservando la seguente figura, si può ricavare il modulo, con la seguente proporzione:
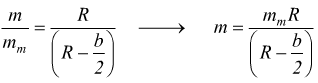
oppure con la seguente formula pratica
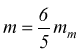
 edutecnica
edutecnica