Equazione della retta
Una generica equazione di primo grado, nelle variabili x ed y è nella forma:
![]() con a e b mai simultaneamente nulli.
con a e b mai simultaneamente nulli.
Dividiamo l'equazione precedente per b:

in quest' ultima poniamo $$m=-a/b$$ e $$q=-c/b$$ ottenendo l'equazione canonica della retta:
![]()
Il diagramma cartesiano dell'equazione precedente è sempre una retta, qualunque
sia il valore dei coefficienti m e q. La forma:
$ax+by+c=0$
viene chiamata equazione della retta in forma
implicita, diversamente dalla $y=mx+q$ che viene chiamata
equazione della retta in forma esplicita.
Se nell'equazione $y=mx+q$ mancano i due coefficienti m e q, la retta che ne rappresenta il diagramma è il luogo dei punti che hanno ordinata uguale a 0,
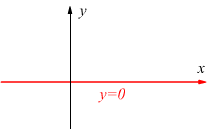
quindi è l'asse delle x, la cui equazione è y=0.
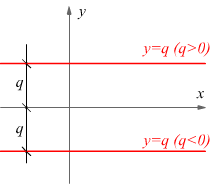
Se soltanto m è nullo si ha: y=q e la rappresentazione grafica di tale espressione
è ancora una retta, parallela all'asse x e distante da esso della quantità
q; infatti solo i punti di questa retta hanno tutti ordinata uguale a q,
e la retta si trova sopra o sotto l'asse x a seconda se q sia positivo o
negativo.
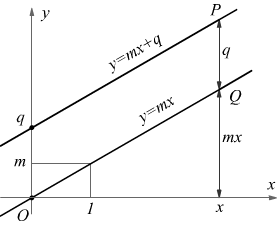
Il caso in cui q=0 corrisponde all'equazione y=mx.
Si nota come l'origine di coordinate O(0,0) e il punto A(1,m) appartengono
alla retta rappresentata dall'equazione (le loro coordinate soddisfano l'equazione).
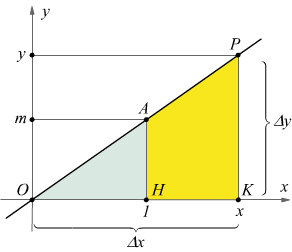
Si verifica poi,che le coordinate di tutti i punti della retta OA soddisfano l'eq. y=mx. Infatti detto P(x,y) un generico punto di tale retta, dalla similitudine dei triangoli rettangoli OKP e OHA risulta:
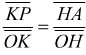 ma
essendo
ma
essendo 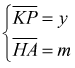 e
e 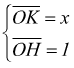 sostituendo
si ha :
sostituendo
si ha :
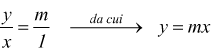
Le coordinate (x;y) di ogni punto della retta OA soddisfano dunque l'equazione y=mx; la rappresentazione grafica della funzione y=mx è una retta passante per l'origine.
Dal disegno si vede che passando dal punto x=0 al generico punto x (scelto arbitrariamente) si ha una variazione della variabile indipendente x pari a Δx a cui corrisponde una proporzionale variazione Δy della variabile dipendente y.
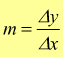
Il coefficiente angolare m può essere definito come il rapporto incrementale tra le due variabili y ed x.
Il coefficiente m può anche essere definito come il rapporto incrementale tra le due variabili y ed x.
• se m> i punti della retta appartengono al 1° e al 3° quadrante,
la y è crescente al crescere di x.
• se m<0 i punti della retta appartengono al 2° e al 4° , la y decresce
al crescere di x.
L'inclinazione della retta rispetto agli assi coordinati dipende soltanto
dal valore di m .
Al variare del coefficiente m varia il rapporto delle coordinate dei punti
della retta; di conseguenza varia l'angolo che la retta forma con l'asse
delle x.
m=coefficiente angolare
Nel caso più generale in cui m≠0 e q≠0 la funzione y=mx+q è sempre
rappresentata da una retta e precisamente dalla retta che incontra l'asse
l'asse y nel punto di ordinata uguale a q e che è parallela alla retta di
equazione y=mx.
q=quota
il parametro q , anche chiamato quota (ordinata all'origine) rappresenta l'intersezione della retta con l'asse delle coordinate y.
Nella y=mx il parametro q è assente, cioè q=0; per questo motivo un'equazione y=mx rappresenta sempre una retta passante per l'origine degli assi.
Si evidenzia in questo caso , come due rette che hanno lo stesso coefficiente angolare m sono parallele.
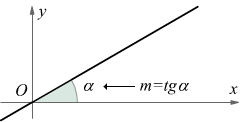
L'inclinazione della retta dipende dal coefficiente angolare m : dal punto di vista geometrico esso può essere facilmente identificato con la tangente dell'angolo α che la retta forma rispetto all'asse x delle ascisse.
Le funzioni riconducibili all'equazione y=mx+q sono sempre delle linee rette, per questo motivo vengono dette funzioni lineari.
Data l'equazione di una retta, è semplicissimo determinarne la collocazione sul piano cartesiano.
Esempio : disegnare la retta di equazione y=2x+1.
Basta porre y=0 e verificare il valore della x quando la retta interseca, appunto, l'asse x;
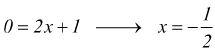 ottenendo
il punto $$P(-1/2;0)$$
ottenendo
il punto $$P(-1/2;0)$$
poi, si pone x=0 verificando il valore della y quando la retta interseca, appunto, l'asse y; questo valore coincide ovviamente con il valore della quota q.
![]() ottenendo
il punto $Q=(0;1)$
ottenendo
il punto $Q=(0;1)$
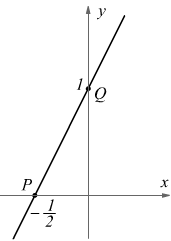
La retta che ci è stata assegnata, passa sicuramente per questi due punti che appartengono alla retta stessa; come ovvio constatare una retta su un piano è completamente identificata quando si conoscono due punti attraverso i quali la retta passa; questi due punti devono appartenere alla retta cioè ne devono soddisfare l'equazione.
m : q :
Rette in posizioni particolari
A La retta parallela all'asse delle ordinate y, rappresenta il luogo dei punti che hanno distanza k costante da quell'asse; la sua equazione è
![]() in
particolare l'equazione dell'asse y è x=0.
in
particolare l'equazione dell'asse y è x=0.
B Il luogo dei punti che hanno distanza costante q dall'asse x è una retta parallela a tale asse la cui equazione è
![]() in
particolare l'equazione dell'asse x è y=0.
in
particolare l'equazione dell'asse x è y=0.
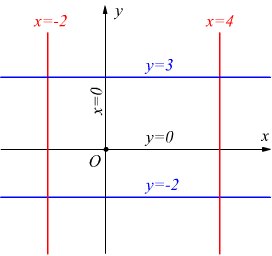
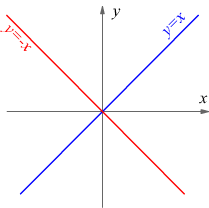
C La bisettrice del 1° e del 3° quadrante è il luogo geometrico dei punti equidistanti dagli assi e perciò dei punti che hanno ascissa ed ordinata uguali tra loro in valore ed in segno, essa ha dunque equazione
![]()
D La bisettrice del 2° e del 4° quadrante è il luogo geometrico dei punti equidistanti dagli assi ma in questo caso, ascissa ed ordinata hanno valori opposti; essa ha quindi equazione
![]()
Equazione del fascio di rette passante per un punto
Se volessimo scrivere l'equazione della retta passante per un punto assegnato P(x1; y1); le coordinate del punto dovrebbero soddisfare l'equazione canonica della retta
![]() deve
essere allora:
deve
essere allora: ![]() sottraendo
membro a membro:
sottraendo
membro a membro:
![]()
Questa è l'equazione della retta richiesta, dove però, il valore di m è indeterminato: al variare di m si ricavano tutte le equazioni delle infinite rette passanti per P(x1; y1). Essa è l'equazione del fascio di rette passante per P(x1; y1).
Esempio : scrivi l'equazione della retta che passa per il punto P(-2;-3) e parallela alla retta di equazione
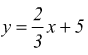
Come detto prima, due rette sono parallele se hanno lo stesso coefficiente angolare che in questo caso è $$m=2/3$$ dunque l'equazione richiesta è:
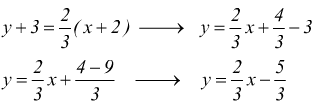
Equazione della retta passante per due punti
Considerando due punti P(x1; y1) e Q(x2; y2) abbiamo detto che l'equazione del fascio di rette di centro P è
![]()
Se facciamo in modo che la retta passi anche per il punto Q, le coordinate di Q devono soddisfare l'equazione precedente.
![]() dividendo
membro a membro le due equazioni precedenti si avrà:
dividendo
membro a membro le due equazioni precedenti si avrà:
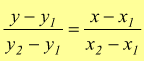
che è l'equazione cercata, cioè, individua la retta passante per i due punti assegnati.
Esempio : trova l'equazione della retta passante per i due punti P1(1;1) P2(-1;2)
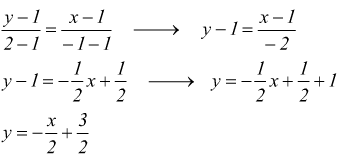
x2 : y1 :
Condizione di perpendicolarità
E' possibile dimostrare che due rette di equazioni y=m1x+q1 e y=mx+q sono perpendicolari quando si verifica l'uguaglianza:

cioè quando il prodotto dei coefficienti angolari è -1. E' sufficiente fare la dimostrazione per le due rette parallele a quelle assegnate di equazioni y=m1x ed y=mx
Supponiamo che le due rette perpendicolari, facciano vedere che risulta
m1m=-1. Sulla retta y=mx, consideriamo il punto A(1,m) e sulla
retta y=m1x, il punto B(-1,m1).
Notiamo dal disegno che i due triangoli OA'A e OBB' sono simili perché hanno
lo stesso angolo α e β uguali, perché complementari dello stesso angolo
γ.
Pertanto avremo :
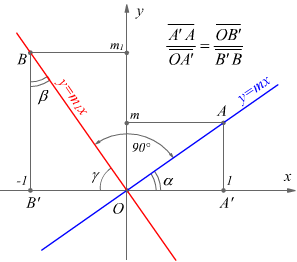
Dato che OA'=1 e OB'=1 sostituendo si ha
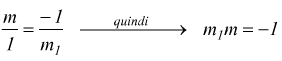
questa è la condizione necessaria e sufficiente affinchè due rette risultino perpendicolari.
Esempio :
scrivi l'equazione della retta passante per il punto P(-2;3) e perpendicolare
alla retta di equazione 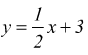
L'equazione del fascio di rette di centro P è ![]()
La perpendicolare alla retta data deve avere coefficiente angolare m1
tale che 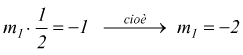
l'equazione della retta richiesta è

Distanza di un punto da una retta
Consideriamo ora il problema di determinare la distanza di un punto P di coordinate xo ed yo da una retta.
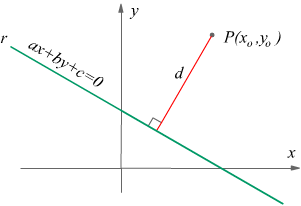
Ricordiamoci che la distanza di un punto P da una retta r è la misura del segmento PH, con H piede della perpendicolare condotta da P alla retta stessa. Indicando con d la distanza del punto P dalla retta r, si ha
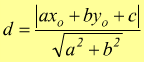 usando
i parametri della forma implicita oppure
usando
i parametri della forma implicita oppure
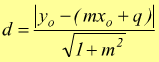 usando
i parametri della forma esplicita
usando
i parametri della forma esplicita
Distanza tra due punti
L'equazione della retta per come è stata definita descrive un luogo geometrico sul piano cartesiano idealmente di lunghezza infinita. Due punti appartenenti ad una retta data, identificano invece, un segmento, cioè una linea retta di lunghezza finita.
Con qualche semplice ragionamento è possibile determinare la lunghezza di tale segmento.
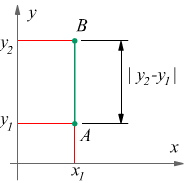
Nel caso i due punti abbiano la stessa ascissa x, il segmento sarebbe verticale, come si vede nel disegno la lunghezza del segmento AB viene identificata dall'uguaglianza
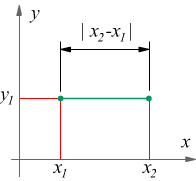
mentre nel caso il segmento sia orizzontale, cioè i due punti abbiano la stessa ordinata la distanza sarà espressa dall'uguaglianza
![]()
La presenza del modulo indica che anche nel caso la differenza tra i due termini produca un valore negativo, esso deve essere considerato positivo; questo perchè, ovviamente, non esistono lunghezze negative.
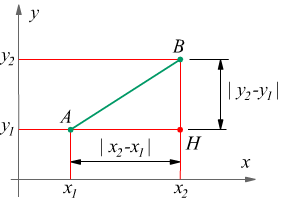
Nel caso più generale in cui A(x1;y1) e B(x2;y2) sono due punti qualsiasi del piano, tracciamo da A la parallela all'asse x e da B la parallela all'asse y. Queste parallele si incontrano nel punto H .
Si riconosce il triangolo rettangolo di vertici ABH; noi siamo interessati alla lunghezza dell'ipotenusa di questo triangolo rettangolo che possiamo trovare con il teorema di Pitagora.
![]() cioè
cioè
![]() ma
dato che |a|2=a2 si può scrivere
ma
dato che |a|2=a2 si può scrivere
![]()
Punto medio di un segmento
Dopo aver trovato il modo di calcolare la lunghezza di un segmento su un piano cartesiano potremo avere la necessità di determinarne il punto medio. Torniamo quindi al segmento definito dalla retta congiungente i due punti A(x1;y1) e B(x2;y2) facendo riferimento al disegno seguente
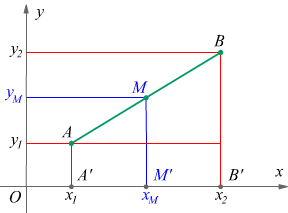
Indicando con M il punto medio, proiettiamo A, B ed M sull'asse x e notiamo che
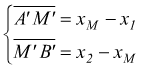 poiché
AM=MB dal teorema di Talete segue A'M'=M'B' dunque
poiché
AM=MB dal teorema di Talete segue A'M'=M'B' dunque
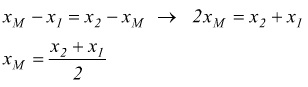
se si procede in modo analogo sulla variabile y si troverebbe
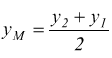
Le coordinate del punto medio M del segmento AB sono pertanto:
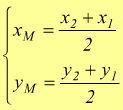
 edutecnica
edutecnica