Insieme dei numeri interi relativi
Nell’insieme N dei numeri naturali non
è possibile eseguire una sottrazione nel caso in cui il minuendo sia minore
del sottraendo.
Si può rimediare a questo inconveniente ampliando la classe dei numeri naturali,
introducendo i numeri negativi.
In questo modo può essere costituito l'insieme Z dei numeri interi relativi che include anche i numeri negativi e che possiamo indicare:
Z={...-3; -2; -1; 0; +1; +2; +3;...}
Un esempio pratico dell'uso dei numeri relativi si ha nel sistema di misurazione della temperatura in gradi Celsius (gradi centigradi) in questo caso lo zero termometrico si ha in corrispondenza alla temperatura del ghiaccio fondente. Noi sappiamo però che è possibile rilevare temperature di 5°C ma occorre precisare se i 5° sono sopra o sotto lo zero dicendo nel primo caso che si hanno +5°C e nel secondo caso -5°C.
Anche quando si misura il tempo, a partire da un dato istante (istante iniziale) occorre precisare se se un altro istante che interessa considerare segue o precede quello iniziale; allora all'istante iniziale si fa corrispondere lo zero e alla misura dell'intervallo di tempo che intercorre tra l'istante iniziale e quello considerato si dà il segno + o il segno - secondo che l'istante considerato segua o preceda quello iniziale.
Nelle operazioni di cassa occorre distinguere se i diversi movimenti di capitale sono delle riscossioni o dei pagamenti e in questo modo possono essere indicati positivi i crediti e negativi i debiti.
Si conclude che i numeri ai quali si premette il segno + opure il segno - possono essere chiamati numeri relativi; in particolare, i numeri preceduti dal segno + si dicono numeri positivi, quelli preceduti dal segno - si dicono numeri negativi.
I numeri positivi, i numeri negativi e lo zero, formano l'insieme dei numeri relativi.
•Il valore assoluto, o modulo, di un numero relativo è il numero stesso privato del segno.
Il valore assoluto di + 3 è 3; il valore assoluto di -5 è 5 e si scrive: |+3|=3 e |-5|=5
Quindi ogni numero relativo possiede queste due caratteristiche: il
modulo ed il segno.
Due numeri relativi che hanno lo stesso segno si dicono
concordi; due numeri relativi che hanno segno diverso si dicono discordi.
Due numeri che hanno lo stesso valore assoluto e segno contrario si possono
chiamare opposti oppure contrari.
Il numero zero è l'opposto di se stesso.
• Due numeri relativi sono uguali, solo se hanno lo stesso segno e lo stesso modulo.
Il confronto tra due numeri relativi può essere fatto tenendo presente a loro rappresentazione geometrica sulla semiretta dei numeri naturali che dopo essere stata ampliata per ospitare i numeri interi relativi è diventata una retta numerica.

Se si vogliono confrontare due numeri relativi a e b, possiamo dire che a è minore di b (scrivendo a<b) se il punto sulla retta numerica associato ad a si trova a sinistra dello stesso punto associato al numero b.
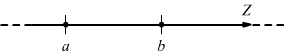 Vi
sono anche dei criteri non visuali
Vi
sono anche dei criteri non visuali
– Ogni numero positivo è maggiore di qualunque numero negativo. +2>-1
o anche -1<2 .
– Di due numeri positivi è maggiore quello che ha valore assoluto maggiore.
+1<+7 o anche +7>+1 .
– Di due numeri negativi è maggiore quello che ha valore assoluto minore.
-3<-1 o anche -1>-3 .
– Lo zero è minore di ogni numero positivo ed è maggiore di ogni numero
negativo.
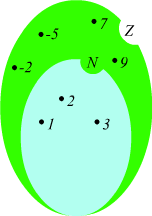
L'insieme dei numeri relativi Z, comprende ed include al suo interno
l'insieme dei numeri naturali N.
L'insieme N, è dunque, un sottoinsieme di Z in senso stretto (non coincide
con Z) i matematici indicano questa condizione con la scrittura: N ⊂
Z.
Addizione in Z
L'addizione con i numeri relativi si indica ponendo il segno + tra i numeri relativi chiusi dentro parentesi, ciascuno con il proprio segno.
La somma di due numeri relativi concordi è il numero relativo che ha lo stesso segno degli addendi e per modulo la somma dei loro moduli.
(+6)+(+8)=+14
(-5)+(-3)=-8
La somma di due numeri relativi discordi è il numero relativo che ha il segno dell'addendo con modulo maggiore e per modulo la differenza dei moduli dei numeri assegnati.
(+8)+(-2)=+6
(+3)+(-12)=-9
da questa caratteristica si deduce che la somma di due numeri opposti è
zero.
(-3)+(+3)=0
• La somma di un numero relativo con lo zero è uguale al numero stesso;
per questo motivo lo zero (0) è considerato l'elemento neutro dei numeri
relativi rispetto all'addizione (come nel caso dei numeri naturali).
(+3)+0=+3
(-7)+0=-7
• Normalmente le operazioni con i numeri relativi si svolgono in modo
meno macchinoso cioè, scrivendoli senza parentesi, uno di seguito all'altro,
ciascuno col proprio segno (eliminando il segno + dell'addizione)
(+5)+(-3)+(-7)+(+12)+(-4)
elimino, ora, il segno + tra le parentesi e anche queste ultime.
+5-3-7+12-4=(+5+12)+(-3-7-4) =(+17)+(-14)=+3
• Quando il primo addendo è positivo, si può anche tralasciare di
scrivere il segno + di esso; ad es. al posto di scrivere
+8+12-10
si scrive di solito
8+12-10.
L'addizione di più numeri relativi gode delle proprietà commutativa e associativa
Proprietà commutativa
La somma di più numeri relativi non cambia comunque si muti l'ordine degli addendi.
![]()
Proprietà associativa
La somma di più numeri relativi non cambia, se ad alcuni essi si sostituisce la loro somma effettuata .
Specifichiamo prima che:
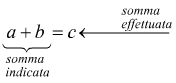
questa proprietà può essere espressa anche attraverso la regola seguente
pratica: in una somma di più numeri relativi, si può racchiudere tra parentesi
un numero qualsiasi di addendi, scrivendo questi numeri con gli stessi segni
che hanno nella somma indicata. Ad es.
+1-8-20+9-12=(1+9)+[(-8)+(-12)]+(20)=
=10+(-20)-20=10-20-20=-30
Si nota come i numeri che si chiudono tra parentesi e che quindi vengono
sostituiti con la somma effettuata, non devono necessariamente occupare
posizioni consecutive, perché in virtù della proprietà commutativa si può
cambiare l'ordine degli addendi, prima di sostituirli con la somma effettuata.
Proprietà dissociativa
La somma di più numeri relativi non cambia, se ad uno di essi si sostituiscono più numeri relativi, la somma dei quali, è uguale al numero soppresso.
-4+12-3=-4+(4+8)+(-8+5)=-4+4+8-8+5=+5
Una regola pratica che si deduce dalle proprietà dell'addizione è che: quando davanti ad una parentesi che racchiude una somma , c'è il segno +, si può togliere la parentesi eliminando il segno + che la precede, lasciando invariati i segni dei suoi addendi.
Altre semplificazioni notevoli sono conseguenza delle proprietà dell'addizione.
9+4-4+7
qui si vede che che ci sono due addendi opposti :+4 ed il -4 e grazie alla
proprietà associativa si vede che essi possono essere eliminati, perché
la somma di due numeri opposti è zero.
Da questa osservazione si ricava la regola generale che dice che se in una
somma ci sono due addendi opposti essi si possono tranquillamente sopprimere
( si dice che i due addendi si "elidono").
La manovra più frequente che si riesce a fare, applicando le proprietà
commutativa ed associativa, consiste nel ridurre una somma di più numeri
relativi all'addizione di due numeri relativi di segno contrario.
Normalmente, si possono scrivere prima tutti i numeri positivi e poi quelli
negativi.
-1+5+10-14+6-8=5+10+6-1-14-8
poi si applica la proprietà associativa separatamente i termini positivi
e a quelli negativi
(5+10+6)+(-1-14-8)=21+(-23)=21-23=-2
• Per eseguire la somma di più numeri relativi si possono sommare separatamente tra loro prima i numeri positivi e quelli negativi, poi si sommano i due numeri relativi discordi che sono stati ottenuti.
Moltiplicazione in Z
Il prodotto tra due numeri relativi è il numero relativo che ha per valore assoluto il prodotto dei valori assoluti dei due numeri assegnati e per segno il + o il - a secondo che i due numeri siano concordi oppure discordi.
|
(+)
|
×
|
(+)
|
=
|
+
|
|
(+)
|
×
|
(-)
|
=
|
-
|
|
(-)
|
×
|
(+)
|
=
|
-
|
|
(-)
|
×
|
(-)
|
=
|
+
|
cioè la regola dei segni.
(+2)·(+3)=+6
(-4)·(-5)=+20
(+3) ·(-7)=-21
(-6) ·(+2)=-12
Regola dell'annullamento di un prodotto
Quando uno dei fattori di un prodotto è zero,
è nullo anche il prodotto. Ad es.
(+3)·0=0 oppure
(-2)·0=0 oppure
0·(+5)=0 oppure
0·(-7)=0
Viceversa, se il prodotto di due fattori è uguale a zero, almeno uno dei due fattori deve essere uguale a zero.
![]()
Il prodotto di un numero relativo per (+1) è uguale al numero stesso; invece, il prodotto di un numero relativo per (-1) è uguale all'opposto di quel numero
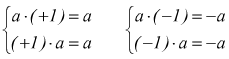
L'elemento neutro rispetto alla moltiplicazione continua ad essere 1; invece ( e lo ripetiamo) il prodotto di un numero per -1 equivale a cambiare il segno al numero assegnato.
Proprietà commutativa
Il prodotto di più numeri relativi non cambia
al mutare dell'ordine dei fattori.
Cioè, rimane la regola a·b=b·a vista per i numeri naturali.
Proprietà associativa
Il prodotto di più numeri relativi non cambia
se ad alcuni di essi si sostituisce il loro prodotto effettuato.
Cioè, rimane la regola (a·b)·c = a·(b·c) vista
per i numeri naturali.
Proprietà distributiva rispetto alla somma
Per moltiplicare una somma algebrica per un numero, o viceversa, si può moltiplicare ciascuno degli addendi della somma per quel numero e poi sommare i prodotti parziali ottenuti.
a·(b+c)=a·b+ a·c
l'operazione inversa: a·b+ a·c=a·(b+c) è il raccoglimento a fattor comune.
Numeri reciproci
Due numeri si dicono reciproci (o inversi) quando il loro prodotto è uguale a +1.
Sottrazione in Z
La sottrazione, nell'insieme Z dei numeri relativi può essere formalizata come già fatto per i numeri naturali. La sottrazione è l'operazione aritmetica che permette di calcolare la differenza tra due numeri di cui il primo è chiamato minuendo e il secondo sottraendo.
La differenza di due numeri nell'insieme Z dei numeri relativi, esiste sempre, ed è il numero che aggiunto al sottraendo fornisce come risultato il minuendo (differenza+sottraendo=minuendo).
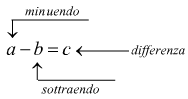
La differenza di due numeri relativi numeri relativi si indica ponendo
tra il primo termine (a ≡ minuendo) ed il secondo termine
(b ≡ sottraendo) il segno -.
La differenza tra i due numeri a e b la indichiamo a-b. Indicando con (-b)
l'opposto di b si avrebbe:
a-b=a+(-b) dunque potremo scrivere le espressioni:
6-2=(+6)-(+2)=+4=4
poi, si può aggiungere che se davanti a qualche termine o parentesi, appare il segno - è come se quella parentesi o quel termine fosse moltiplicato per -1; dunque:
(+8)-(-15)=(+8)+(-1)·(-15)=(+8)+(+15)=+23
In base alla regola della moltiplicazione che prevede che un numero moltiplicato per (-1) corrisponde all'opposto di quel numero.
Nell'insieme Z dei numeri relativi la sottrazione si può sempre eseguire, anche quando i sottraendo è maggiore (in modulo) del minuendo; al contrario di quanto accade nell'insieme N dei numeri naturali dove si fa uso solo di numeri positivi.
Proprietà invariantiva della sottrazione
La sottrazione tra due numeri relativi gode della proprietà invariantiva, cioè, la differenza tra due numeri non cambia aggiungendo o togliendo uno stesso numero sia al minuendo che al sottraendo
![]()
anche questa, già vista nei numeri naturali. Ad es.
(-8)-(+5)= (-8+2)-(+5+2)
Siccome la sottrazione di due numeri relativi può essere ricondotta ad
una addizione, l'addizione e la sottrazione di numeri relativi possono essere
considerati una unica operazione: 6-9 può rappresentare
sia la somma (+6)+(-9) dei due numeri relativi (+6) e (-9)
sia la differenza (+6)-(+9) dei numeri relativi (+6) e (+9)
Un insieme di numeri relativi legati tra loro da segni di addizione e sottrazione possono formare una struttura chiamata somma algebrica . Ad es.:
(+2)-(+3)+(-5)-(-4)-(+7)
è una somma algebrica perchè in base alle definizioni appena date può essere
ricondotta ad una somma che indichiamo
(+2)+(-3)+(-5)+(+4)+(-7)
da qui si vede come la somma algebrica non è altro che una somma di numeri
relativi; anche se poi la sua rappresentazione più frequente è
2-3-5+4-7
Cambiando espressione: se ora eseguiamo la sottrazione:
-10-(3+4-5)
dovremo sommare al -10 l'opposto della somma tra parentesi ma quest'ultima
operazione si ottiene cambiando il segno a tutti i termini inclusi nella
parentesi stessa
-10+(-3-4+5)
per la regola pratica della proprietà dissociativa della somma avremo
-10-3-4+5
Si conclude che : per togliere da un numero una somma algebrica, basta aggiungere
a quel numero gli addendi della somma algebrica con il segno cambiato.
Da qui, deriva una ulteriore regola: se davanti ad una parentesi c'è il segno - si può togliere la parentesi a patto di cambiare segno a tutti i termini della somma.
Si può facilmente intuire che questa regola può essere applicata anche in senso contrario.
7+(4-2+3)=7-(-4+2-3)
Divisione in Z
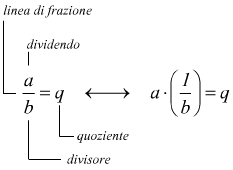
Il quoziente di due numeri relativi, di cui
il secondo (il divisore) diverso da zero, si ottiene moltiplicando il
primo (dividendo) per il reciproco del secondo.
Il quoziente tra due numeri relativi si indica interponendo tra il primo
termine (dividendo) ed il secondo (divisore) il segno : oppure la linea
di frazione indifferentemente, con tre possibili scritture equivalenti
Avendo ricondotto la divisione ad una moltiplicazione, ricordiamo che anche in questo caso valgono le regole dei segni. In sintesi: il quoziente di due numeri relativi ha per valore assoluto il quoziente dei loro valori assoluti e per segno il + o il - a secondo che i due numeri abbiano lo stesso segno oppure segno contrario.
Rimangono le regole
Proprietà invariantiva della divisione
Il quoziente tra due numeri relativi non cambia se vengono moltiplicati entrambi per uno stesso numero diverso da zero.
Questà proprietà importantissima, è alla base delle semplificazioni che si possono fare sulle frazioni
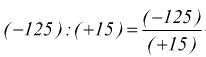
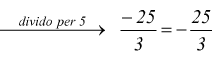
Come conseguenza immediata si nota che il quoziente di due numeri relativi resta invariato se si cambiano simultaneamente i segni al dividendo e al divisore
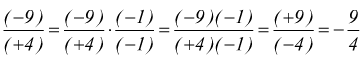
è semplice; è come se moltiplicassimo sia il numeratore che il denominatore per -1; si può fare, perché (-1)/(-1)=1; cioè; è come moltiplicare la frazione originaria per 1, e qualsiasi numero moltiplicato per 1 rimane invariato (1 elemento neutro rispetto alla moltiplicazione).
Quest'ultima regola viene usata spesso per ragioni di comodità, perché quando c'è una frazione si preferisce sempre avere un denominatore positivo.
Una seconda articolazione di questa proprietà è: Per dividere un prodotto per un numero si può dividere uno solo dei fattori per quel numero e moltiplicare gli altri fattori per il quoziente ottenuto
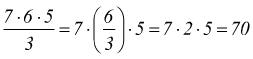
Proprietà distributiva della divisione rispetto alla somma
Per dividere una somma per un numero si può dividere ciascun addendo della somma per quel numero e poi sommare i quozienti parziali ottenuti.
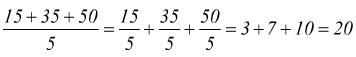
Raccoglimento a fattor comune
Basandoci sulla proprietà distributiva della moltiplicazione rispetto alla somma (algebrica)
(+2)(10-3)=20-6 possiamo anche scrivere il contrario 20-6=2 (10-3)
si chiama raccoglimento a fattor comune perché è stato raccolto il fattor comune (il 2 in questo caso) dei termini della somma algebrica.
Questa operazione può anche essere eseguita in presenza di quozienti indicati: quando tutti i termini di una somma algebrica contengono uno stesso fattore, la somma è uguale al prodotto del fattore comune per la somma dei quozienti ottenuti
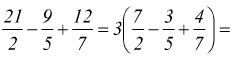
Riassumendo:
L'insieme dei numeri interi relativi si indica con la lettera Z. L'insieme
Z comprende:
• i numeri interi negativi;
• lo zero (che non ha segno)
• i numeri interi positivi.
Potremo notare come nell'insieme Z sia possibile definire le varie operazioni
aritmetiche e come sia sempre possibile eseguire anche l'operazione di sottrazione
(non sempre possibile in N). Quindi:
• l'insieme Z è chiuso rispetto alla sottrazione (si può sempre fare)
• l'insieme Z è un ampliamento dell'insieme N.
Espressioni
Una espressione aritmetica è un insieme di numeri naturali legati tra loro
da segni di operazioni.
Essa è , dunque, una qualunque scrittura che indica delle operazioni
aritmetiche da eseguire con i numeri relativi.
Calcolare una espressione algebrica significa trovare il numero relativo
che rapppresenta il risultato delle operazioni indicate.
Non necessariamente le operazioni che ci sono devono essere eseguite nell'ordine
in cui si presentano.Ad es. nell'espressione
4+3·5
è errato eseguire prima la somma 4+3 e poi moltiplicare il risultato per
5.
Si deve prima eseguire la moltiplicazione
3·5 e dopo sommare 4 al risultato
4+3·5=4+15=19
La moltiplicazione ha priorità sulla addizione.
Il grado di priorità, cioè, l'ordine di precedenza delle operazioni è:
1) elevamento a potenza
2) moltiplicazione e divisione
3) addizione e sottrazione
Le operazioni che hanno lo stesso grado di priorità, come moltiplicazioni e divisioni oppure addizioni e sottrazioni si devono eseguire nell'ordine in cui sono indicate.
In una espressione, una volta calcolate le potenze si eseguiranno, sempre nell'ordine in cui sono indicate, moltiplicazioni e divisioni; da ultimo, sempre nell'ordine in cui sono indicate, verranno eseguite addizioni e sottrazioni.
E' ammessa un'unica eccezione: se in una espressione è indicata una somma di tre o più numeri, oppure il prodotto di tre o più numeri, vale la proprietà associativa, dunque il risultato non cambia anche se le operazioni vengono svolte in ordine inverso da quello indicato.
esempio: calcola il valore dell'espressione 12×2:6
L'espressione contiene solo moltiplicazioni e divisioni, cioè, operazioni
con lo stesso grado di priorità. Eseguiamo allora, le operazioni nell'ordine
indicato:
12×2:6=24:6=4
esempio: calcola il valore dell'espressione 15+7×2×5+20
Si devono eseguire prima le moltiplicazioni
15+7×2×5+20=15+70+20=105
esempio: calcola il valore dell'espressione 3+8×52:4-40:23
Calcoliamo prima le potenze 3+8×25:4-40:8
adesso facciamo le moltiplicazioni
3+200:4-40:8
adesso facciamo le divisioni 3+50-5=48
Supponiamo di voler risolvere l'espressione
5+4×3
con questa scrittura, dovremmo eseguire prima la moltiplicazione di 4×3
e poi addizionare 5 al risultato.
Se invece si volesse prima eseguire la somma 5+4 e poi la moltiplicazione
per 3, si dovrebbe scrivere
(5+3)×3
Ad es. nell'espressione 12×(5-2) bisogna prima eseguire la sottrazione
5-2 e poi moltiplicare per 12 il risultato:
12×(5-2)=12×3=36
allo stesso modo nell'espressione (3+4+1)2
si deve prima eseguire la somma indicata nella parentesi e poi l'elevamento
a potenza; per cui
(3+4+1)2=82=64
Esistono vari tipi di parentesi
( ← parentesi tonde
[ ← parentesi quadre
{ ← parentesi graffe
hanno tutte la stessa funzione: cambiare l'ordine di priorità delle operazioni
all'interno di una espressione.
E' possibile usare anche solo parentesi tonde.
Per togliere le parentesi da un'espressione si devono dapprima eseguire
le operazioni contenute nelle coppie di parentesi più interne (che non contengono
ulteriori parentesi al loro interno) scrivendo al loro posto il risultato
ottenuto.
Alla fine, quando l'espressione non contiene più parentesi si procede nei
calcoli rispettando l'ordine di priorità delle varie operazioni.
Vediamo l'espressione
{7+[(6+5×3)+4]:(2+3)×(5+7)} (7-4) avremo

Qualche suggerimento sulle modalità di soluzione di una espressione aritmetica è riportato in questa pagina.
 edutecnica
edutecnica