Disequazioni con valore assoluto

      

Dalla definizione di valore assoluto di un numero reale x può essere dedotta l'importante proprietà:

|x| > 0 per x ≠ 0 così che |x| ≥ 0 ∀x ∈ R

questa regola viene applicata anche nel caso in cui all'interno della segnatura di modulo appaia una generica espressione algebrica :

|f(x)| >0 per f(x) ≠ 0 in modo tale che |f(x)| ≥ 0 ∀x ∈ R

questi criteri risultano importanti nel caso in cui si debbano risolvere disequazioni contenenti espressioni in modulo. Ad esempio

|x–3| < 0 risulta essere una disequazione impossibile con un insieme delle soluzioni vuoto S ≡ ∅ ;
mentre la disequazione |x–3| ≤ 0 ha come unica soluzione x=3.

|x–2| ≥ 0 è invece sempre verificata mentre la disequazione |x–2| > 0 viene soddisfatta per x ≠ 2, infatti se x=2 la disequazione diventa 0 > 0 che è falsa.

Sempre in base alla definizione di valore assoluto, è evidente che disequazioni del tipo:

|x–3| > –2 oppure |x²+7x–8| > –3    sono sempre verificate mentre le disequazioni

|2x–3| < –2 e |x⁵–x²| < –5   sono impossibili, cioè non ammettono soluzioni (l'insieme delle loro soluzioni è vuoto S ≡ ∅ ).

Questi sono casi in cui al secondo membro vi è un valore ( che d'ora in poi chiameremo k) che è negativo o nullo; tuttavia può capitare di dover risolvere disequazioni del tipo:

|f(x)| < k con k > 0
|f(x)| > k sempre con > 0

|f(x)|<k con k>0

      

Ammettendo, dunque, k∈R⁺ (k appartenente all'insieme dei numeri reali positivi) dalla definizione di valore assoluto avremo

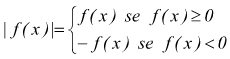
quindi la disequazione |f(x)| < k equivale ai due sistemi

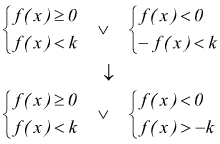
La disequazione, sarà risolta per   in pratica avremo:      riassumendo:

Attenzione; in questo caso la soluzione è l'intersezione delle soluzioni delle due disequazioni: 

|f(x)|>k con k>0

      

Se consideriamo la disequazione |f(x)| > k con k∈R⁺ avremo i due sistemi

      

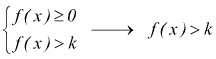
oppure

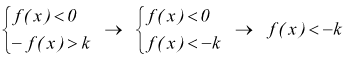
Quindi la disequazione |f(x)| > k è verificata per f(x) > k ∨ f(x) < –k. In sintesi

In questo caso la soluzione è l'unione delle soluzioni delle due disequazioni:

Se immaginiamo che f(x) sia una funzione rappresenta sul piano cartesiano xy, le zone non colorate sono quelle dove la f(x) è ammissibile.

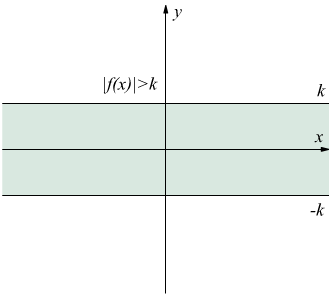
Ad esempio:     equivale a dire mettendo a sistema:

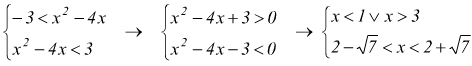
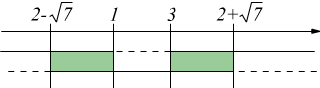
se ne ricava:       

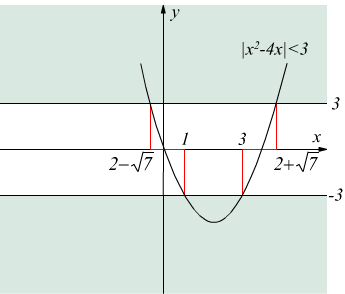
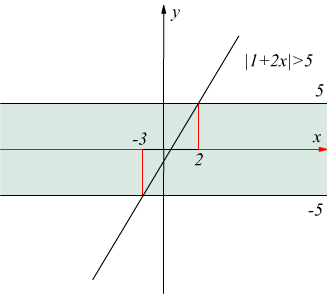
Altro esempio:  equivale a dire  mettendo a sistema:

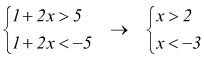     la soluzione è