Disequazioni frazionarie

Il metodo seguito per la risoluzione di questo tipo di disequazioni è completamente sulla traccia di quello illustrato per ultimo per le disequazioni di II°grado:

1] Si portano tutti i termini al I°membro, in modo che al II° vi sia solo lo 0.

2] Si cerca di impostare l'espressione al I°membro come prodotto di polinomi di grado non superiore al 2° o come un'unica frazione che abbia per numeratore e per denominatore polinomi di grado 1 o 2.

3] Si studia il segno di ciascun polinomio ottenuti come detto in precedenza.

4] Si disegna uno schema grafico riassuntivo della variazione dei segni dei polinomi al variare della x.

5] Tenendo conto che il segno di un rapporto o di un prodotto è positivo se i fattori negativi sono in numero pari , negativo se i fattori negativi sono in numero dispari, si stabilisce il segno che assume l'espressione (sempre che tale valore non annulli il denominatore della frazione al I° membro).

6] Si deduce l'insieme delle soluzioni della disequazione.

Esempio:

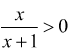
il numeratore è positivo quando x>0
il denominatore è positivo quando x+1>0   => x> -1


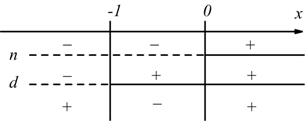
Nel grafico è stato evidenziato il segno del numeratore n e del denominatore d. Dato che il rapporto di due fattori è positivo quando il segno di questi è concorde, otteniamo che la disequazione è vera (è positiva) per: