Circonferenza

La circonferenza è il luogo dei punti del piano equidistanti da un punto fisso chiamato centro.
La distanza tra ognuno dei punti ed il centro è chiamato raggio della circonferenza.

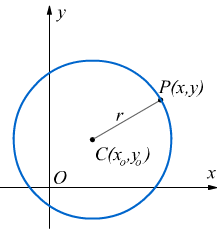
Possiamo individuare una circonferenza solo quando sono note le coordinate del centro C(x_o;y_o) ed il raggio r.
Osservando il disegno, si riconosce che per un generico punto P(x;y) collocato sulla circonferenza, che si trova sempre alla stessa distanza r dal centro C(x_o;y_o) deve valere la relazione

✘

Quest'ultima formula è l'equazione della circonferenza di centro C(x_o;y_o) e raggio r.

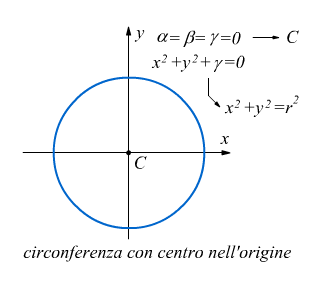
Nel caso particolare in cui il centro coincide con l'origine O (x_o =0 ed y_o=0) si ha l'equazione della circonferenza con centro nell'origine e raggio r.

Se sviluppiamo i quadrati nella relazione ✘ si ha

si pone

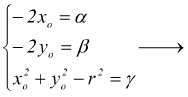
Quest'ultima, è l'equazione della circonferenza in forma canonica (normale) dalla quale si possono ricavare velocemente le coordinate del centro C.

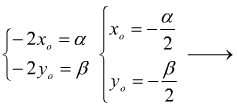
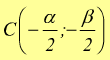
e la misura del raggio

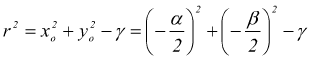ottenendo

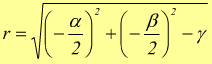
Solo se 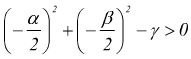si ha l'equazione di un circonferenza.

Se tale espressione è nulla si dice che la circonferenza è degenere nel suo centro.

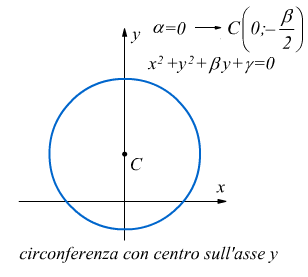
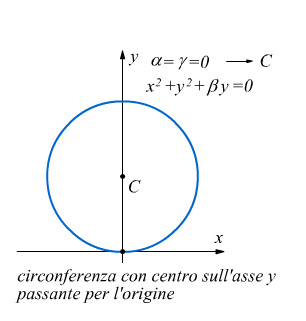
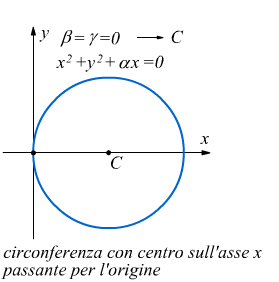
• Se γ=0 l'equazione diventa

e la circonferenza passa per l'origine O(0;0) perché come si vede le coordinate dell'origine soddisfano la sua equazione

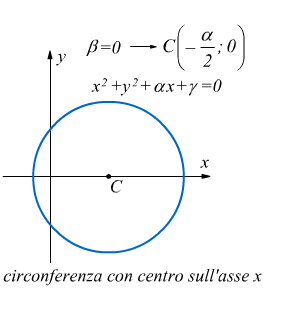
• Se α=0 avremo

che se ammette soluzioni, rappresenta una circonferenza con centro in 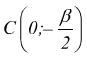sull'asse y delle ordinate.
Un riassunto delle varie eventualità è qui sotto riportato:

Posizione reciproca tra retta e circonferenza

Per trovare le intersezioni di una circonferenza con una retta del suo piano basta risolvere il sistema formato dalle due equazioni: quella della retta e quella della circonferenza.

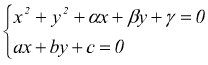
Se ci sono due soluzioni distinte, la retta è secante la circonferenza (cioè la taglia come si vede nel primo disegno).
Se le due soluzioni sono coincidenti, la retta è tangente la circonferenza, se invece non ci sono soluzioni la retta è esterna alla circonferenza.

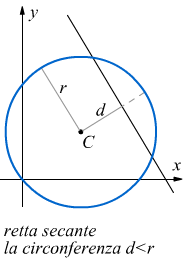
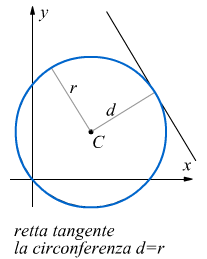
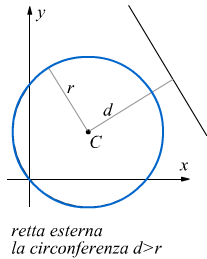
Come appare dai disegni la retta è secante, tangente oppure esterna alla circonferenza se la distanza d della retta dal centro C della circonferenza è rispettivamente minore, uguale oppure maggiore del raggio d della circonferenza.

α : β : γ :

m :      q :

xMin :      xMax :

yMin :      yMax :

Circonferenza passante per tre punti

Esiste un teorema della geometria piana che afferma che dati tre punti non allineati, per essi, passa una ed una sola circonferenza.
Trovare l'equazione della circonferenza passante per tre punti, rimane dunque, un problema tradizionale e ricorrente.
Dato che i tre punti devono appartenere alla circonferenza cercata, essi devono soddisfare la sua equazione canonica.
Note le coordinate dei tre punti A(x_A;Y_A) B(x_B;y_B) e C(x_C;y_C) si intuisce che deve essere risolto il problema di tre equazioni in tre incognite qui riportato (ved. es.11).

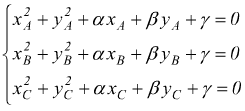
ricavando le tre incognite α , &brta; e γ.

Posizione tra due circonferenze

Un altro problema frequente è quello della ricerca di eventuali punti di intersezione tra due circonferenze.
Anche in questo caso bisogna fare il sistema tra le equazioni delle due circonferenze.

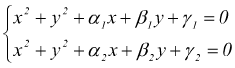
Sottraendo membro a membro la prima dalla seconda si ottiene

Quella ottenuta è l'equazione implicita di una retta a cui viene dato il nome di asse radicale.

In questo modo si è ricondotti alla ricerca dei punti di intersezione di una delle due rette con l'asse radicale.
Si può facilmente constatare che l'asse radicale è perpendicolare alla congiungente dei centri delle due circonferenze.

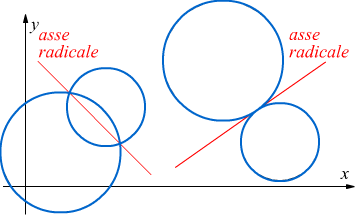
• Se vi sono due punti di intersezione distinti le due circonferenze sono secanti.
• Se vi sono due punti di intersezione coincidenti le due circonferenze sono tangenti (internamente o esternamente).
• Se non vi sono soluzioni le due circonferenze non hanno punti in comune.