Sinusoidi e fasori
Quando si vuole rappresentare un generico segnale sinusoidale la notazione privilegiata usata in elettrotecnica è
![]() [
I ]
[
I ]
Questa formula deve essere seguita dall'unità di misura della grandezza
che si vuole descrivere [V] [A] etc..
La rappresentazione grafica della funzione e=e(t) sarà la seguente
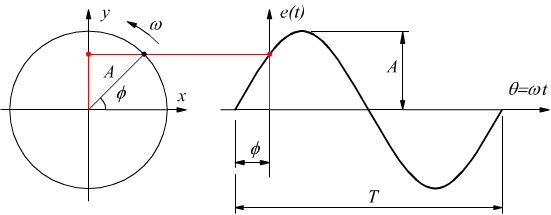
Si vede come e(t)≡y(t) è la rappresentazione al passare del tempo
della proiezione ortogonale del segmento di lunghezza A rotante attorno
all'origine del piano x-y sull'asse delle ordinate. Abbiamo già visto
come si può generare un segnale di questo tipo.
Si tratta di un moto armonico e la formula [ I ] contiene tutte le informazioni
:
A=ampiezza dell'onda
ɸ=fase iniziale [rad]
ω=2π/T=2π·f= pulsazione [rad/s]
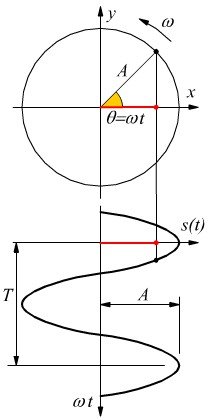
Il moto armonico si
ottiene proiettando su un diametro le posizioni di un punto materiale
che si muove di moto circolare uniforme lungo una circonferenza.
Generalmente, il moto armonico si esprime con la relazione
![]() [
II ]
[
II ]
Dai disegni si vede come 'A' sia l'ampiezza dell'oscillazione che poi coincide con il raggio della circonferenza [s(t)≡x(t)]che viene percorsa dal punto materiale con velocità angolare ω=cost.
Va detto, che è indifferente esprimere il moto armonico tramite il seno piuttosto che col coseno, infatti, la funzione seno differisce dalla funzione coseno solo per una differenza di π/2 rispetto ad una eventuale fase iniziale; come dire
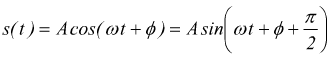 In
ogni caso, la e(t) è riconducibile alla derivata di s(t)
In
ogni caso, la e(t) è riconducibile alla derivata di s(t)
ma se la s(t) rappresenta uno spazio, la s'(t) è una velocità.
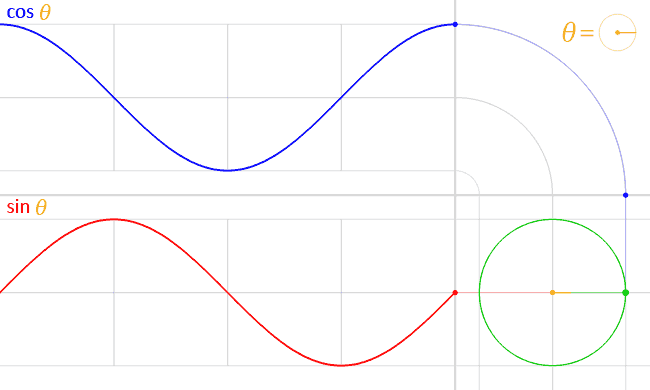
Per rappresentare grandezze elettriche, si privilegia la forma [I] perchè
ci ricordiamo come una differenza di potenziale ΔV può essere
causata da un conduttore che si muove in un campo magnetico costante
tramite la legge di Faraday :
![]()
B=campo magnetico
l= lunghezza del conduttore
v=velocità del conduttore che sta tagliando le linee di flusso magnetico.
Come si è visto nel caso di una spira rotante di sezione S
![]()
ma l'energia elettrica, viene sempre prodotta, industrialmente, da macchine rotanti, ecco perchè alla fine indichiamo il generatore di tensione in regime alternato sinusoidale con la notazione
![]() [ V ]
[ V ]
La tensione elettrica è associata ad una velocità [si preferisce la
funzione sin(ω·t)] meccanica che è poi quella del conduttore
in moto che taglia perpendicolarmente le linee di flusso di un campo
magnetico costante B.
Dopo questa osservazione, le formule definite nella pagina sui circuiti
in alternata, possono sembrare un po' più plausibili, non fosse che
ad un certo punto, iniziano ad apparire i numeri complessi.
Ogni tanto, qualcuno si chiede il perché: da dove provengono i numeri
complessi?
Torniamo all'equazione [II] rappresentativa il moto armonico; essa
è già stata ottenuta per
l'oscillatore
armonico integrando una equazione differenziale del secondo ordine
omogenea
![]()
che descrive le oscillazioni di una molla;bisogna tener conto che si tratta di un'equazione differenziale del secondo ordine omogenea
![]()
ha come equazione caratteristica il trinomio di secondo grado
![]()
Dall'Analisi Matematica si sa che se il discriminante ![]() l'equazione
caratteristica ammette come integrale generale
l'equazione
caratteristica ammette come integrale generale
![]() con
c1 e c2 costanti arbitrarie.
con
c1 e c2 costanti arbitrarie.
Nel caso ![]() l'eq.caratteristica
ammette le due soluzioni reali coincidenti
l'eq.caratteristica
ammette le due soluzioni reali coincidenti
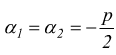 e
l'integrale dell'equazione è
e
l'integrale dell'equazione è
![]()
Nel caso ![]() l'equazione
caratteristica ammette le due soluzioni complesse coniugate:
l'equazione
caratteristica ammette le due soluzioni complesse coniugate:
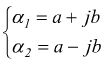 e
l'integrale generale diventa
e
l'integrale generale diventa
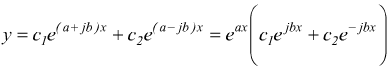
a questo punto bisogna ricordarsi delle formule di Eulero 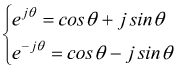 si
avrebbe
si
avrebbe
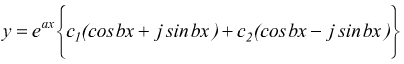
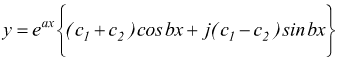 [ III ]
[ III ]
se a c1 e c2 vengono assegnati i valori complessi coniugati :
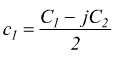 e
e 
l'integrale generale diventa con C1 e C2 costanti reali arbitrarie.
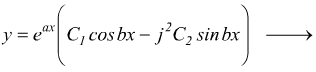
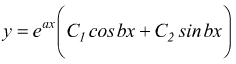
essendo j2=-1.
nota: normalmente l'operatore immaginario si indica con la lettera 'i' ma in elettrotecnica questo simbolo si confonde facilmente con la corrente. Dunque si usa il simbolo j.
Può essere riscritta in un altro modo
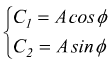 quindi
quindi
![]()
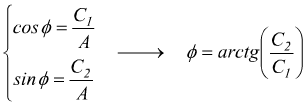 sostituendo
si ha
sostituendo
si ha
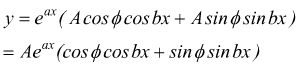
![]() [
IV ]
[
IV ]
con A e ɸ costanti arbitrarie.
Quest'ultima relazione è la stessa che descrive l'oscillatore
smorzato. se a<0 viene descritta da una sinusoide inviluppata
in una curva esponenziale decrescente.
Al contrario se a>0 la sinusoide avrebbe delle escursioni di ampiezza
progressivamente crescenti anche se è difficile immaginare un caso del
genere nella realtà (si avrebbe un sistema instabile).
Invece, se l'equazione differenziale è del tipo ![]() si
ha p=0 → a=0
si
ha p=0 → a=0
![]()
le radici dell'equazione caratteristica sono complesse coniugate, immaginarie
pure.
L'equazione può essere ricondotta alla formula generale del moto armonico:
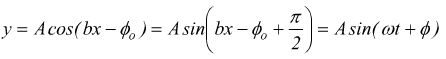
ɸ=ɸ/2-ɸo =cost.
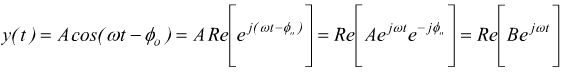
con B=Aexp(-jɸo). Invece per la forma sinusoidale
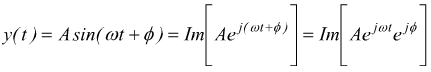 il
numero complesso
il
numero complesso
![]()
è il fasore corrispondente alla funzione y(t)
alla pulsazione ω.
Il fasore, è una 'fotografia' istantanea della y(t=0): indipendente
dal tempo, dalla frequenza e dalla pulsazione
(tutte le grandezze di un sistema lineare sono isofrequenziali dunque
hanno la stessa pulsazione).
Esso corrisponde alla rappresentazione polare di un numero
complesso.
Come numero complesso, un fasore può essere disegnato sul piano di Gauss
sotto forma di vettore
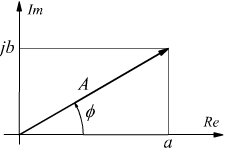
Per la formula di Eulero
![]()
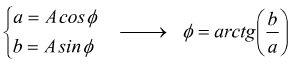 con
con
![]()
La rappresentazione in forma polare tipica di un fasore è vantaggiosa quando bisogna eseguire il prodotto tra due sinusoidi.
![]()
![]()
perchè per le proprietà degli esponenziali
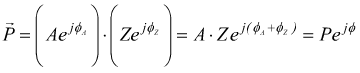
o il rapporto tra due sinusoidi
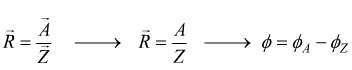
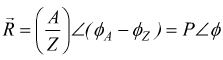
Nel caso della somma o differenza tra sinusoidi si è però obbligati a trasformare il fasore nella sua forma simbolica binomiale
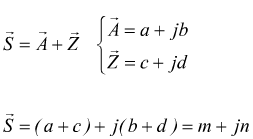
per poi tornare alla forma polare
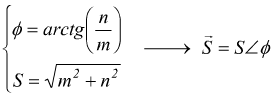
 edutecnica
edutecnica