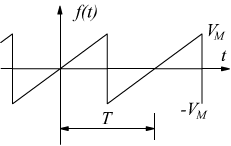
Teorema di Fourier
Secondo il teorema di Fourier, tutti i segnali periodici, di qualunque
forma d'onda, possono essere considerati come il risultato della sovrapposizione
di più segnali sinusoidali di opportune ampiezze e frequenze, opportunamente
sfasati tra loro.
Una funzione f(t) di periodo T e frequenza f=1/T
può essere espressa da una serie del tipo:
![]()
che si può anche scrivere come
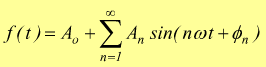
Il primo termine di pulsazione ω di ampiezza A1
e di fase ɸ1 viene chiamato prima armonica
o armonica fondamentale, il secondo termine è la seconda armonica e
così via.
Si vede come la prima armonica ha frequenza pari alla frequenza della
funzione, la seconda armonica ha frequenza doppia, la terza ha frequenza
tripla e così via.
I requisiti richiesti alla f(t) per essere sviluppata secondo
la serie di Fourier, sono quelli di essere generalmente continua e sommabile
nell'intervallo ( 0,T ) cioè se la f(t) è integrabile
nell'intervallo ( 0,T ) e questo integrale ha valore finito,
la f(t) può essere espressa secondo la serie di Fourier.
Sviluppando il generico termine con la formula di addizione
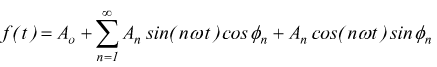
poniamo 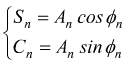
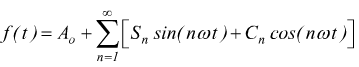

Integriamo ora, entrambi i membri della precedente relazione dall'istante t=0 a t=T
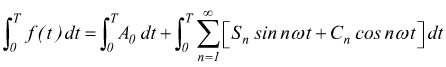
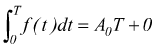
questo perchè l'integrale di una funzione sinusoidale o cosinusoidale esteso al periodo T è uguale a zero.Otteniamo dunque:
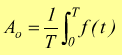 valor
medio della f(t).
valor
medio della f(t).
Per le componenti Sn e Cn è possibile dimostrare che:

Sapendo poi, che le forma d'onda periodiche sono usate come vettrici e codificatrici di informazione risulta utile conoscere il valore efficace del segnale analizzato:
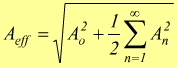
Sono obbligatorie alcune osservazioni.
Se la f(t) è una funzione periodica pari,
cioè se f(t)=f(–t) lo sviluppo in serie di
Fourier si riduce ad una serie di soli coseni, essendo i termini Sn
uguali a zero.
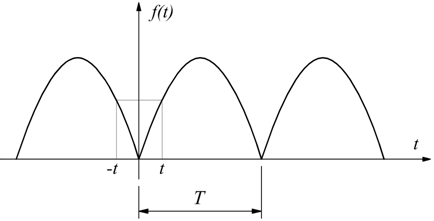
in questo caso si ha:
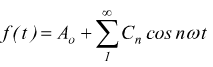
Se invece la f(t) è una funzione periodica dispari, cioè se f(t)=–f(–t) lo sviluppo in serie di Fourier si riduce ad una serie di soli seni essendo i termini Cn uguali a zero.
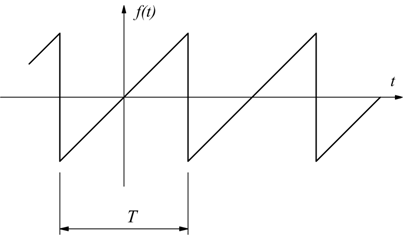
in questo caso si ha:
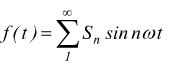
Inoltre, per definizione di funzione dispari, il termine Ao è in questo caso nullo.
Analisi spettrale
Usando il teorema di Fourier si può analizzare un segnale periodico qualsiasi
e determinare le sue componenti armoniche.
Le ampiezze e le fasi di ciascuna armonica possono essere riportate su
grafici che rappresentano lo spettro di ampiezza e lo spettro di fase
del segnale analizzato.
Nel disegno sottoriportato, è riprodotta un'onda quadra di valor medio
Ao=0,5 costruita con le sue prime sette componenti armoniche,di
fianco è illustrato il relativo spettro di ampiezze (si nota l'assenza
di armoniche pari).
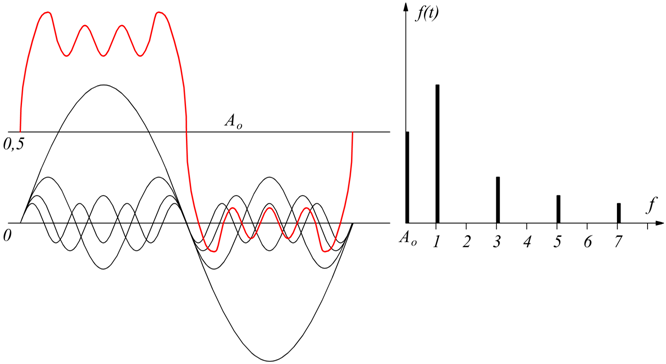
Come si nota, non è facile disegnare un segnale che riguarda una serie
di Fourier in modo soddisfacente, questo perchè bisogna tener
conto del contributo di ciascuna componente della serie.
In genere, conviene controllare l'andamento con appositi programmi calcolatori.
come questa
applet Java.
In linea di massima si può notare che pur essendo infiniti i termini
della serie le componenti armoniche di frequenza elevata rispetto alla
fondamentale presentano ampiezze progressivamente decrescenti e quindi
il loro contributo può essere in certi casi trascurato.
Ovviamente, tanto maggiore è il numero delle armoniche considerato e
tanto maggiore è la precisione con cui la somma delle componenti approssima
il segnale.
Riportiamo di seguito gli sviluppi in serie di Fourier per i principali
segnali con 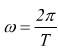
|
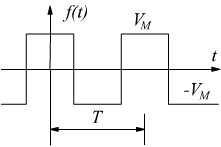
Onda quadra |
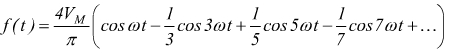 |
|
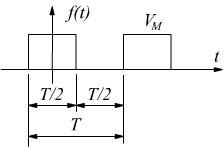
Onda quadra unipolare |
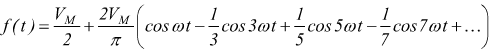 |
|
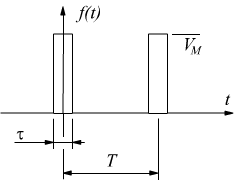
Treno di impulsi |
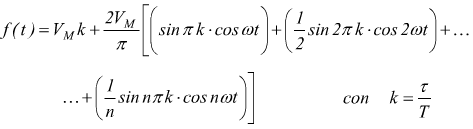 |
|
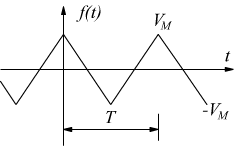
Onda triangolare |
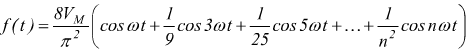 |
|
Dente di sega |
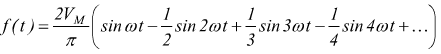 |
Le considerazioni fatte sui segnali periodici possono essere estese
ai segnali non periodici se,invece di esprimere la funzione mediante
la serie di Fourier,la si rappresenta mediante l'integrale di Fourier.
In questo caso le frequenze che compongono il segnale non presentano
valori discreti ma uno spettro continuo di valori dalla frequenza zero
a infinito.
 edutecnica
edutecnica