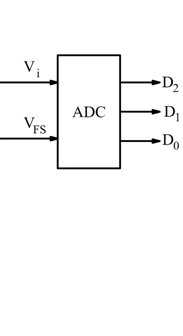
ADC conversione analogico-digitale
Gli ADC o convertitori analogico-difitale, convertono i valori di tensione in ingresso nel numero corrispondente espresso in binario. La Risoluzione (R) di un convertitore A/D è definita come la minima variazione della grandezza analogica in ingresso che provoca una variazione di un LSB (Least Significant Bit= bit meno significativo) nel numero di uscita: tale variazione è definita come quanto (Q ). La risoluzione R di un ADC coincide, dunque, col quanto Q.
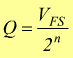
con VFS=Tensione di fondo scala; essa è una tensione di riferimento
fornita al convertitore: essa individua il massimo valore in ingresso convertibile
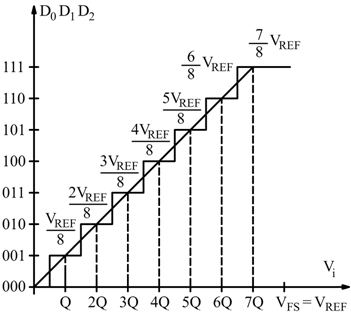
in binario. In figura è rappresentato il comportamento di un ADC a 3 bit;
in uscita, dovranno essere rappresentati N=2n=23=8
numeri compreso lo 0.
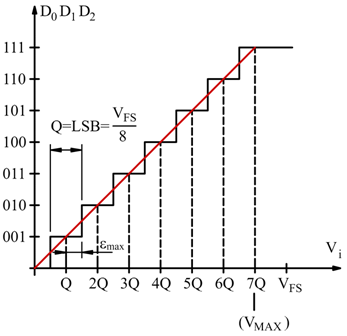
Si nota come un valore di tensione in ingresso Vi=Q venga convertito
in uscita col valore (001)2, così come tutti i valori compresi
fra Q/2e 3Q/2. Viene così introdotto l'errore di quantizzazione ε
max.
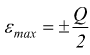
Il massimo valore di tensione in ingresso che può essere convertito in binario
con errore ε=0:
![]()
Convertitore ADC Flash
Chiamato anche convertitore con priorità, ha il compito di individuare la
soglia di valore di tensione maggiore, tra quelle superate dalla tensione
di ingresso per poi generare la corrispondente codifica binaria.
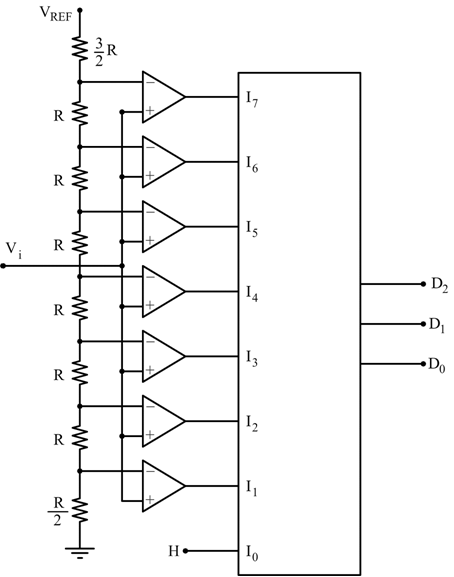
Qui è invece riportato un convertitore (minimale) a 2 bit. Ad ogni resistenza
che si trova al morsetto non invertente di un operazionale si ha un salto
di tensione pari al valore del quanto Q. Il circuito combinatorio usato
per la codifica è molto semplice. In questo caso:
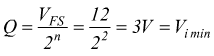
Questa è la variazione minima della tensione di ingresso per permettere una variazione del bit meno significativo (LSB) in uscita.
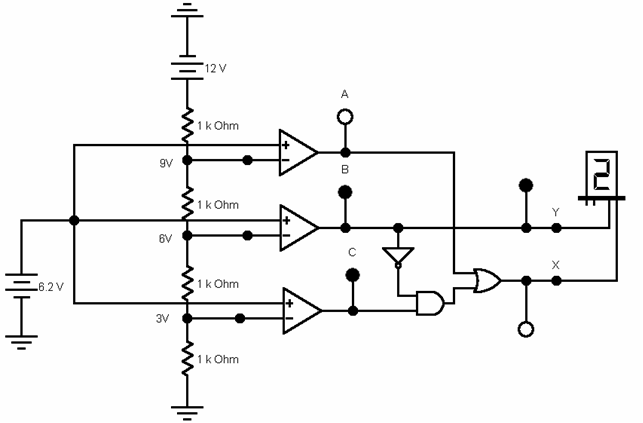
Ad esempio quando la tensione di ingresso è di 9,5V avremo:
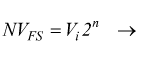
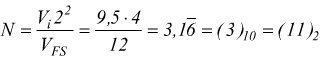
infatti la massima tensione che può essere convertita in binario è:
![]()
Il circuito restituisce 0 in uscita se Vi<3V restituisce
1 se 3V < Vi < 6V, restituisce 2 se 6V < Vi <9V restituisce
3 se Vi>9V. Non ha un grande precisione, ma la tecnica usata
è la stessa anche per convertitori di maggior precisione.
Il campionamento e la conversione dei segnali
In figura è rappresentato un sistema di acquisizione e ricostruzione
per un singolo segnale analogico, i blocchi tratteggiati non sono sempre
necessari .
Per fare in modo che l'informazione acquisita durante il processo non
venga deteriorata dalla conversione in digitale occorre risolvere qualche
problema:
Se il segnale analogico all'ingresso dell'ADC varia molto velocemente
durante la conversione, il valore della tensione a cui è associato il
risultato potrebbe non essere individuabile con precisione ; a seconda
della velocità di variazione del segnale e della risoluzione del convertitore
può essere necessario inserire un circuito Sample and Hold (S/H) a monte
dell'ADC.
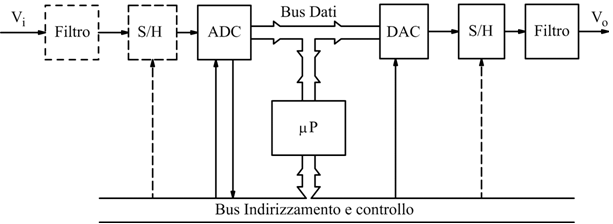
Il segnale all'uscita del DAC è a gradini; per "arrotondare" la forma
d'onda e renderla uguale all'originale è generalmente necessario porre
dopo il DAC un FILTRO PASSA-BASSO.
- Dato che la conversione richiede un certo tempo (Tc), non
è possibile convertire in digitale i valori assunti in ogni istante dal
segnale analogico d'ingresso, ma solo quelli in corrispondenza di una
successione discreta di istanti di tempo. Il problema sta nell'individuare
il massimo intervallo di tempo tra una conversione e quella successiva
, che garantisce ancora la ricostruibilità del segnale originale; la risposta
a quest'ultimo quesito è data dal
Teorema di Shannon
Se fs è la frequenza di campionamento del modulo S/H ed fmax è la frequenza massima del segnale da campionare, il segnale in questione può essere ricostruito se è soddisfatta la condizione:
![]()
Sample and hold (S/H)
Sample and hold significa "campiona" e "mantieni"; lo scopo di questo circuito è quello di acquisire la tensione di ingresso in un determinato istante (campionamento) e di mantenerlo invariato all'uscita fino ad una nuova lettura.
Il circuito che implementa tale funzione è il seguente:
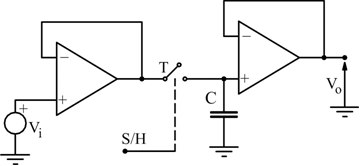
Nella catena di conversione analogico-digitale il circuito S/H precede il convertitore. Il circuito S/H non è sempre indispensabile, la sua presenza dipende dalla velocità di variazione del segnale da convertire. La regola che deve essere rispettata è:
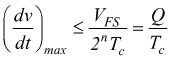
La massima velocità di variazione del segnale deve essere inferiore o uguale al rapporto fra il quanto e il tempo di conversione Tc; n è il numero di bit del convertitore.
Il tempo di conversione è l'intervallo di tempo che passa fra l'istante in cui in ingresso si presenta un valore di tensione stabile e quello in cui sulle uscite appare il corrispondente valore binario.
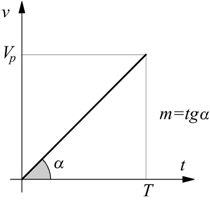
Nel caso di un segnale a rampa è piuttosto semplice, osservando che
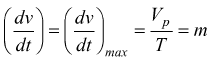
nel caso di un segnale sinusoidale del tipo ![]() si
ha:
si
ha:
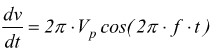
il massimo (la massima variazione) è::
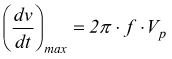
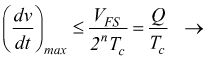
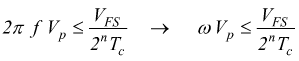
Quindi per i segnali sinusoidali se vale la condizione:
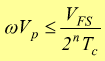
si può evitare di usare un modulo S/H.
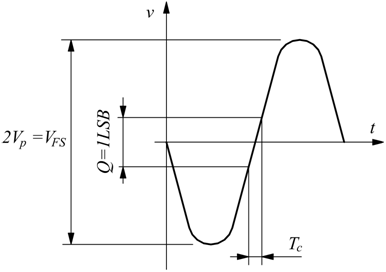
Se ipotizziamo che il valore picco-picco della tensione sinusoidale da convertire abbia il massimo valore convertibile, cioè 2Vp=VFS avremo:
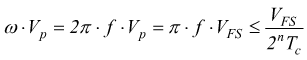 si
avrà:
si
avrà:
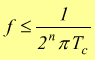
Si può evitare l'uso di un modulo S/H per l'acquisizione dei segnali sinusoidali solo se vengono rispettate queste condizioni.
Esiste l'eventualità che si debbano campionare più segnali simultaneamente con lo stesso convertitore, si applica, usualmente, una tecnica di time-sharing che utilizza un multiplexer analogico.
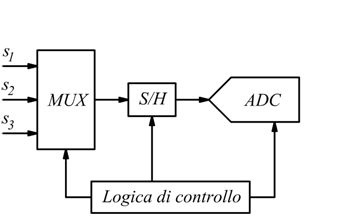
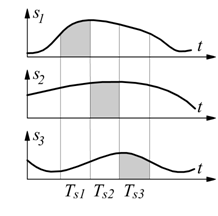
ad intervalli di tempo regolari i segnali analogici in ingresso vengono smistati verso il sistema di acquisizione e campionati . Se gli intervalli di campionamento sono gli stessi:
![]()
deve essere soddisfatta la relazione:
![]() con
con
Ts=tempo di campionamento
Tc=tempo di conversione
N=numero di canali
 edutecnica
edutecnica