Adattamento di modelli probabilistici a distribuzioni empiriche
Gli studiosi di statistica si sono sempre posti il problema di associare le osservazioni di fenomeni concreti a schemi teorici classici. Il problema della 'bontà dell'adattamento' può essere risolto con approcci diversi anche se il metodo del test del chi-quadro rappresenta ancora la tecnica più diffusa per la sua generalità e per i molteplici tipi di confronto che permette di effettuare.
Test chi-quadro
Il metodo consiste in una procedura di confronto tra le frequenze empiriche osservate e le frequenze teoriche; se abbiamo:
n : il numero totale di elementi del campione
k : le modalità della distribuzione
fi :le frequenze assolute empiriche osservate
pi : le probabilità teoriche di modalità i
n·pi : le frequenze assolute teoriche di modalità i
χ2 : è una variabile di distribuzione
χ2 .
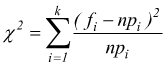
Per applicare correttamente il test occorre che nessuna frequenza teorica sia minore di 5. Se dal calcolo risulta che qualche frequenza teorica è minore di 5, per effettuare il confronto bisogna raggruppare due o più modalità; k è dunque, il numero di modalità (classi) finali che si ottengono.
Il numero di gradi di libertà ν delle distribuzione chi-quadro risulta essere
ν=k-1 se la distribuzione delle frequenze teoriche
può essere determinata senza usare dati campionari.
ν=k-1-m se la distribuzione delle frequenze teoriche
può essere determinata stimando m parametri della popolazione tramite i
valori campionari.
Fissato un valore critico
χc2 legato ad un fissato
livello di significatività per un determinato
ν : numero di gradi di libertà, se:
χ2 < χc2
l'approssimazione è accettabile.
Esempio: adattamento di una distribuzione uniforme
Si vuole verificare se un dado è truccato ad un livello di significatività
del 5%.
Il dado viene lanciato per n=60 volte; la tabella di comparazione tra
le frequenze empiriche ottenute e quelle teoriche è la seguente:
| valore | freq.empirica | freq.teorica |
| 1 | 11 | 10 |
| 2 | 9 | 10 |
| 3 | 6 | 10 |
| 4 | 14 | 10 |
| 5 | 13 | 10 |
| 6 | 7 | 10 |
La soluzione di questo tipo di problema è facilitato dall'uso di fogli di calcolo
ma normalmente, durante il compito in classe, si può usare solo
la calcolatrice e la tabella
del chi-quadro.
In questo caso, ciascuna frequenza teorica vale 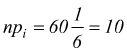 .
Facciamo il test:
.
Facciamo il test:
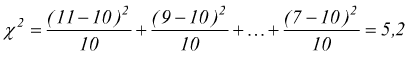
Osservando la tabella della coda di destra il valore di χ2
per ν=5 in corrispondenza del valore di probabilità
0,05 si ha :
χc2=11,07 > 5,2 =χ2
l'approssimazione alla distribuzione uniforme è accettabile.
Esempio: adattamento di una distribuzione
binomiale
Viene eseguita una rilevazione per studiare il numero di nascite maschili
in famiglie con 5 figli, esaminando in totale n=1000 famiglie ottenendo
le frequenze empiriche
| num.maschi | 0 | 1 | 2 | 3 | 4 | 5 |
| freq.emp. | 30 | 140 | 316 | 309 | 174 | 31 |
Si chiede di adattare ai dati empirici ottenuti una distribuzione binomiale ad un livello di significatività del 5%.
Questa volta valutiamo la probabilità: 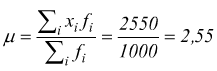
poi 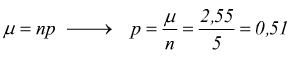
calcolando i vari valori della distribuzione 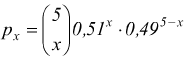 si ha
si ha
po=0,0282 ; p1=0,1470 p2=0,3060 ; p3=0,3185 ; p4=0,1657 ; p5=0,0345
dalle probabilità otteniamo le frequenze teoriche
| num.maschi | 0 | 1 | 2 | 3 | 4 | 5 |
| freq.teo. | 28 | 147 | 306 | 318 | 166 | 35 |
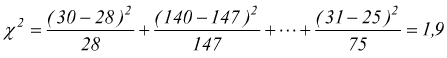
Sono k=6 osservazioni ed m=1 perché le frequenze teoriche sono state determinate studiando la probabilità attraverso i dati campionari; i gradi di libertà sono: ν=k-1-m=6-1-1=4
Dall'esame della coda superiore della distribuzione chi-quadro
ad un livello di significatività dello 0,05 si ha
χc2=9,49 > 1,9 =χ2
l'approssimazione alla distribuzione binomiale è accettabile.
Esempio: adattamento di una distribuzione
di Poisson
Vengono esaminate 500 macchinari prodotti da una certa fabbrica ed è
stata constatata la seguente distribuzione del numero di difetti per
ciascuna macchina:
| num.difetti | 0 | 1 | 2 | 3 | 4 |
| num.pezzi | 225 | 183 | 64 | 23 | 5 |
Si adatti una distribuzione di Poisson con livello di significatività del 5%.
Calcoliamo la media
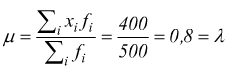
Calcoliamo i vari valori della distribuzione con la formula
di Poisson 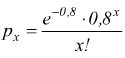
po=0,4493 ; p1=0,3594 ; p2=0,1438 ; p3=0,0383 ; p4=0,0077
queste appena ottenute sono le probabilità teoriche; le frequenze conseguenti sono
fo=500·no=225
f1=500·n1=180
f2=500·n2=72
f3=500·n3=19
f4=500·n4=4
Qui, dobbiamo fare un pò di attenzione, perché l'ultima frequenza teorica è 4 (< 5) quindi le ultime due modalità devono essere raggruppate.
| num difetti | freq.empiriche | freq.teoriche |
| 0 | 225 | 225 |
| 1 | 183 | 180 |
| 2 | 64 | 72 |
| 3 | 28 | 23 |
calcoliamo χ2.
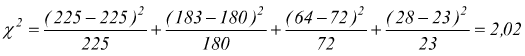
m=1 perché il valor medio è stato ottenuto dai dati sperimentali; mentre per le osservazioni vale l'ultima tabella, cioè k=4. Il numero di gradi di libertà è ν=k-1-m=4-1-1=2 dalla coda superiore della distribuzione chi-quadro si vede che
![]()
χc2=5,99 > 2,02 =χ2 l'approssimazione alla distribuzione di Poisson è considerata soddisfacente.
Esempio: adattamento di una distribuzione normale
Viene misurata la statura di 1000 soggetti maschi che hanno tutti la
stessa età, ottenendo la seguente descrizione
| statura | num. |
| 145< | 1 |
| 145-150 | 3 |
| 150-155 | 27 |
| 155-160 | 100 |
| 150-165 | 231 |
| 165-170 | 287 |
| 170-175 | 220 |
| 175-180 | 101 |
| 180-185 | 24 |
| 185-190 | 5 |
| >190 | 1 |
A ciascuna modalità viene assegnato il valore intermedio e in modo
analogo alla classe aperta più alta viene assegnato il valore 192,5
a quella aperta inferiore 142,5.
Adattiamo la distribuzione con una normale ad un livello di significatività
del 5%.
Calcoliamo la media
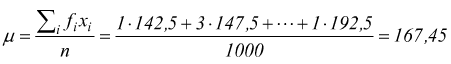
poi otteniamo la varianza e la deviazione standard
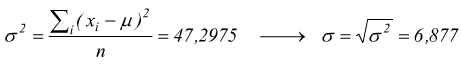
trasformiamo gli estremi degli intervalli nella variabile z standardizzata
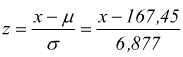
Si ottiene la seguente tabella dove possono essere riportati anche i valori arrotondati delle frequenze teoriche
| classi | freq.empiriche | zmin | zmax | prob. | freq.teoriche |
| 145< | 1 | -3,26 | 0,0006 | 1 | |
| 145-150 | 3 | -3,26 | -2,54 | 0,005 | 5 |
| 150-155 | 27 | -2,54 | -1,81 | 0,0296 | 30 |
| 155-160 | 100 | -1,81 | -1,08 | 0,1050 | 105 |
| 160-165 | 231 | -1,08 | -0,36 | 0,2194 | 219 |
| 165-170 | 287 | -0,36 | 0,37 | 0,2852 | 285 |
| 170-175 | 220 | 0,37 | 1,1 | 0,2197 | 220 |
| 175-180 | 101 | 1,1 | 1,82 | 0,1013 | 101 |
| 180-185 | 24 | 1,82 | 2,55 | 0,029 | 29 |
| 185-190 | 5 | 2,55 | 3,28 | 0,0049 | 5 |
| >190 | 1 | 3,28 | 0,0005 | 0 |
Bisogna raggruppare le prime e le ultime due modalità perché la prima e l'ultima classe hanno frequenza teorica minore di 5. Le osservazioni diventano dunque k=9 m=2 perché dai dati empirici sono state usate media e varianza. ν=k-1-m=9-1-2=6 .
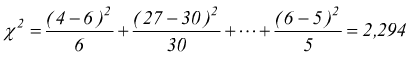
ad un livello di significatività del 5% con 6 gradi di libertà, risulta dalla tabella del chi-quadro
χ0,952=12,6
Dato che χc2=12,6 > 2,294 =χ2 l'approssimazione alla distribuzione normale è da considerare buona.
 edutecnica
edutecnica